[科普中国]-扩频码序列

扩频码序列是指扩频码的二进制序列，它是很窄的脉冲码序列，其码速率是很高的。1

在扩频通信中常需要用高码速率的窄脉冲序列，这是针对扩频码序列的波形而言，并未涉及码的结构和如何产生等问题，现在实际中用的最多的是伪随机码，或称为PN码。这类码序列最重要的特性是具有近似于随机信号的性能。因为噪声具有完全的随机性，也就是说具有近似于噪声的性能。但是，真正的随机信号和噪声是不能重复再现和产生的，只能产生一种周期性的脉冲信号来近似随机噪声的性能，故称为随机码。2

基本特性一般来说，理想的扩频码序列应具有如下特性：

（1）有尖锐的自相关特性；

（2）尽可能小的互相关值；

（3）足够多的序列数；

（4）有尽可能大的序列复杂度；

（5）序列平衡；

（6）工程上易于实现。2

伪随机序列在扩频通信中通常需要高码速的窄脉冲序列作为扩频码，实际上用的最多的是伪随机码序列，或称为伪噪声（PN）码序列。这类码序列最重要的特性是具有近似于随机信号的性能。按照香农信息论，在高斯白噪声信道上，最佳的信号是具有白噪声统计特性的信号，其原因是高斯白噪声具有最大的随机性。但是，真正的随机信号和噪声是不能重复再现和产生的。我们只能产生一种周期性的脉冲信号来近似随机噪声的性能，故称为伪随机码或PN码。2

对伪随机码最基本的要求是具有随机性。这种随机性可以用自相关函数来衡量。自相关函数可以表示信号与其自身相移以后的相似性。2

特点在工程上常用二元{0,1}序列组成伪噪声（PN）码。它具有如下特点：

（1）每一周期内，0和1出现的次数近似相等；

（2）每一周期内，长度为n比特的游程出现的次数比长度为n+1比特游程次数多一倍；

（3）序列具有双值系相关函数；3

伪随机信号扩频技术是选用具有上述伪随机特性的码序列与待传信息流波形相乘或序列模2加之后的复合信号，对射频载波进行调制，然后送入信道进行传输。因此，作为扩频函数的伪随机信号，应具有以下特点：

（1）伪随机信号必须具有尖锐的自相关函数，而互相关函数应接近于零；

（2）有足够长的码周期，以确保抗侦破、抗干扰的要求；

（3）有足够多的独立地址数，以便满足码分多址的要求；

（4）工程上易于产生、加工、复制和控制。3

常用的伪随机序列扩频码序列是伪随机序列，最简单的、最常见的、使用最多的是m码序列或Gold码序列。

1.m序列。

m序列是在一定级数的位移寄存器情况下，所能产生周期最长的PN码。由于m序列容易产生，规律性强，有许多优良的性能，所以在扩频通信中最早获得广泛的应用。m序列是由多位级移寄存器或其它延迟元件通过线性反馈产生的最长的码序列。在二进制位移寄存器发生器中，若n为级数，则能产生的最大长度的码序列为 位。m序列的最大长度决定于位移寄存器的级数，而码的结构决定于反馈抽头的位置和数量。不同的抽头组合可以产生不同长度和不同结构的码序列。有的抽头组合并不能产生最长周期的序列。对于何种抽头能产生何种长度和结构的码序列，已经进行了大量的研究工作。现在已经得到3~100级m序列发生器的连接图和所产生的的m序列的结构。3

m序列有如下性质：

（1）在m序列中的一个周期内“1”的数目比“0”的数目多1位。

（2）在一个序列中连续出现的相同码称为一个游程，连码的个数称为游程的长度。m序列中共有 个游程，其中长度为1的游程占游程总数的1/2，长度为2的游程占游程总数的1/4，长度为3的游程占游程总数的1/8，依次类推，长度为k的游程占 。其中最长的游程是n个连1码，次长的游程是n-1个连0码。

（3）m序列的自相关函数由下式计算： ，其中A为0的位数，D为1的位数。

（4）m序列和其移位后的序列逐位模2相加，所得的序列还是m序列，只是相移不同而已。

（5）m序列发生器中移位寄存器的各种状态，除全0状态外，其他状态只在m序列中出现一次。

（6）m序列发生器中，并不是任何抽头组合都能产生m序列。

在上述m序列的前三个性质正是其随机性的表现。后三个性质在实际应用中都很有用。3

2.Gold码序列。

Gold序列是1967年R.Gold在m序列基础上提出并分析的一种特性较好的伪随机序列，它是由两个码长相等、码时钟速率相同的m序列优选对通过模2相加而构成的。

通过设置m序列发生器B的不同初始状态，可以得到不同的Gold序列，由于总共有m-1个不同的相对移位(Q为m序列的级数)，加上原有的两个m序列，可以产生共m+1个Gold序列。

Gold码序列是一种基于m序列的码序列，具有较优良的自相关和互相关特性，产生的序列数多。Gold码的自相关性不如m序列，具有三值自相关特性；互相关性比m序列要好，但还没有达到最佳。

扩频码序列的相关性选用随机信号或具有噪声性能的信号来传输信息是因为许多理论研究表明，在信号传输中各种信号之间的差别性能越大越好。这样任意两个信号不容易混淆，也就是说，相互之间不容易发生干扰，不会发生误判。理想的传输信号的信号形式应是类似于噪声的随机信号，因为取任何时间上不同的两段噪声比较都不会完全相似。它们代表两种信号，其差别性就会最大。4

在数学上是用自相关函数来表示信号和它自身相移以后的相似性的。随机信号的自相关函数可定义为：

φ=

若a 0，则φ=0；若a=0，则φ=常数。式中。 为信号的时间函数，a为时间延迟。

上式的物理概念是 与其相对延迟的a的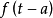 来比较：如二者不完全重叠，即a 0，则乘积的积分为0；若两者完全重叠，即a=0，则乘积的积分为一常数。

因此上式中值得大小可用来表征 与自身延迟后的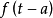 的相关性，故称为自相关函数。4