[科普中国]-动载荷

简介

在工程实际中，有多高速运行的构件，如涡轮机的长叶片旋转时由离心惯性力引起的应力可达相当大的数值；高速转动的砂轮由于离心惯性力而有可能炸裂；汽锤在锻造坯件时，瞬间的冲出载荷能使锤杆的应力高出静应力几倍到几十倍。这种由加速度引起的载荷一般称为动载荷。1

动荷问题一般加速度问题一般加速度问题（包括线加速与角加速），此时尚未引起材料性质的改变，仍可用静荷强度的许用应力，处理此类问题的基本方法是达朗伯原理。

冲击问题构件受极大速度的冲击载荷作用，将引起材料力学性能的很大改变。由于问题的瞬时性与复杂性，工程上常采用基于能量守恒原理的能量法进行简化分析计算。

振动与疲劳问题构件内材料质点的应力作周期性变化。它将引起材料强度的明显变化，并导致构件疲劳破坏。2

动载荷与静载荷构件所承受的载荷由零开始缓慢地增加到某一值后，就保持不变，在加载过程中，构件内各点的加速度很小，可以忽略不计。因此，可认为构件自始至终处于平衡状态。这类问题称为静载荷问题。3

联系试验结果表明，材料在动载荷下的弹性性能基本上与静载荷下的相同，因此，只要应力不超过比例极限，胡克定律仍适用于动载荷下应力、应变的计算，弹性模量也与静载荷下的数值相同。3

区别静载荷和动载荷对于构件的作用是不同的。例如起重机中以加速度提升的绳索。当物体静止不动或以等速上升时，绳索所受拉力等于物体的重量，物体的重量对绳索为静载荷作用。但是如果绳索吊着物体以加速度上升，绳索就要受到较大的拉力。这时物体的重力便引起了动载荷作用。

动载荷应用在工程中，构件受动载荷作用的例子很多。例如，内燃机的连杆、机器的飞轮等，在工作时它们的每一微小部分都有相当大的加速度，因此是动载荷问题。当发生碰撞时，载荷在极短的时间内作用在构件上，在构件中所引起的应力可能很大，而材料的强度性质也与静载荷作用时不同，这种应力称为冲击应力。此外，当载荷作用在构件上时，如果载荷的大小经常作周期性的改变，材料的强度性质也将不同，这种载荷作用下的应力成为交变应力。

动载荷计算物体一般加速度时的动荷问题惯性力与动静法：做加速度运动物体的惯性力大小等于物体的质量m和加速度a的乘积，方向与a相反。假想在每一具有加速度的运动质点上加上惯性力，则物体（质点系）作用的原力系与惯性力系将组成平衡力系。这样就可以把动力问题形式上作为静力学问题来处理，这就是达朗伯原理。

冲击问题工程上采用偏于保守的能量平衡方程来近似估算被冲击物与受冲击物所受冲击载荷与冲击应力。冲击系统能量平衡方程：

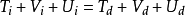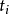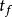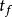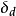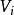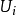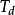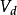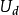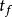此处下标i表示冲击物与受冲击构件发生冲击前那一瞬时的各量。下标d为冲击过程结束那一瞬时的各量，瞬时受冲击构件达到最大冲击变形。、、为瞬时系统的动能、重力势能和弹性变形能。、、 为瞬时系统的动能、重力势能和弹性变形能。