[科普中国]-极限尺寸

极限尺寸的解释包容原则与极限尺寸

包容原则应用于单一要素时，在尺寸公差数值或公差代号后必须加注符号E。此时极限尺寸的检验应符合泰勒原则。

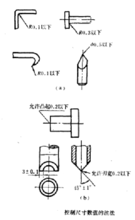
1905年，美国人W.泰勒（William Taylor）提出“螺纹量规改进”这一专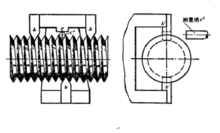利，如右图所示。

通端量规由三个测头b组成，经过通端量规检验合格的螺纹，还需要进行止端检验。止端检验的方法是先将下侧测头b与外螺纹的小径接触，然后观察测量销c'是否能塞进量规与上侧平面c与外螺纹小径之间的空隙，如果塞不进去，则螺纹为合格。

从符合泰勒原则的检验方法可以看出，其最大实体尺寸是MMC边界尺寸，由极限量规的通端控制，理论上“通规”是长度等于被测要素结合长度的完全圆柱表面（全形量规）。最小实体尺寸是局部实际尺寸，由极限量规的止端控制，“止规”是具有量面为两点状的表面（非全形量规）2。

最大实体原则与极限尺寸采用最大实体原则以后，如把最大实体尺寸解释为MMC边界尺寸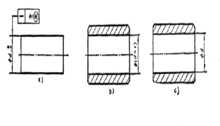，生产上将会引起混乱。如右图所示，销轴在最大实体状态时还允许有t的直线度误差，实效尺寸为 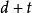，综合量规如右图所示。已如前述，凡被综合量规接受的零件均能保证装配互换性。但是按泰勒原则设计的“通规”来检验尺寸公差时，一定会拒收作用尺寸大于d而小于 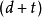的零件。由此可见，有一部分能被综合量规接收，可以满足装配互换性的零件，有一部分会被极限量规拒收作为废品，这显然是不合理的，也是极不经济的。所以采用最大实体原则时，把最大实体尺寸解释为MMC边界尺寸是错误的。应该和最小实体尺寸一样解释为局部实际尺寸，采用两点测量法进行检验才是合理的。

独立原则与极限尺寸独立原则不考虑尺寸公差与形位公差的相互依赖关系，因此必须用不控制实际形状的两点测量法检验尺寸。此时最大实体尺寸和最小实体尺寸都应该解释为局部实际尺寸，这样才能保证独立原则的应用2。

极限尺寸判断原则极限尺寸的判断原则（即泰勒原则）：

孔或轴的作用尺寸不允许超过最大实体尺寸。即对于孔，其作用尺寸应不小于最小极限尺寸；对于轴，则应不大于最大极限尺寸。

在任何位置上的实际尺寸不允许超过最小实体尺寸，即对于孔，其实际尺寸应不大于最大极限尺寸；对于轴，则应不小于最小极限尺寸。

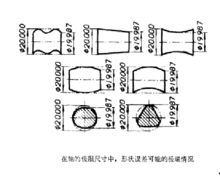
在孔的极限尺寸中，例如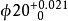 ，形状误差可能的极端情况见下图一；

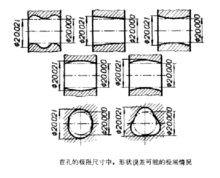
在轴的极限尺寸中，例如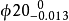 ，形状误差可能的极端情况如下图二3。

极限尺寸注法与使用性能或装配精度要求有关的极限尺寸常采用以下几种注法：

直接注出最大和最小极限尺寸

注出极限尺寸后，可不用任何说明，如下图所示。

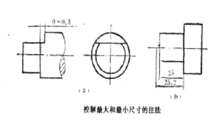
2.控制尺寸数值在某一尺寸之下

除注出尺寸数值外，还需附以文字注解，如下图所示。

3.只注出最大或最小极限尺寸

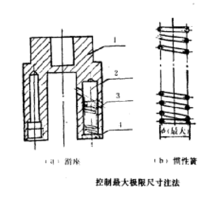
在弹簧装配中，由于弹簧有内、外表面定位的区别，通常需要在弹簧零件图上控制其内、外径的极限尺寸，以保证其可靠装配。

如下图所示，为了方便惯性簧3在滑座1孔内装配，要求惯性簧的外径略小于滑座孔的孔径，这时只要控制惯性簧外径的最大极限尺寸即可。

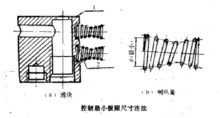
又如下图所示，为了使喇叭簧2大端装入滑块1孔内，不致掉出来，要求弹簧大端外径比滑块孔外径要稍大些，这样才能装紧可靠。这时应控制弹簧大端内径的最小极限尺寸4。