[科普中国]-图像复原

概述

图像复原技术主要是针对成像过程中的“退化”而提出来的，而成像过程中的“退化”现象主要指成像系统受到各种因素的影响，诸如成像系统的散焦、设备与物体间存在相对运动或者是器材的固有缺陷等，导致图像的质量不能够达到理想要求。图像的复原和图像的增强存在类似的地方，它也是为了提高图像的整体质量。但是与图像复原技术相比，图像增强技术重在对比度的拉伸，其主要的目的在于根据观看者得喜好来对图像进行处理，提供给观看者乐于接受的图像，而图像复原技术则是通过去模糊函数去除图像中的模糊部分，还原图像的本真。其主要采用的方式是同采用退化图像的某种所谓的先验知识来对已退化图像进行修复或者是重建，就复原过程来看可以将之视为图像退化的一个逆向过程。图像的复原，首先要对图像退化的整个过程加以适当的估计，在此基础上建立近似的退化数学模型，之后还需要对模型进行适当的修正，以对退化过程出现的失真进行补偿，以保证复原之后所得到的图像趋近于原始图像，实现图像的最优化。但是在图像退化模糊的过程中，噪声与干扰同时存在，这给图像的复原带来了诸多的不确定性。

涉及内容基本思路图像复原的基本思路：先建立退化的数学模型，然后根据该模型对退化图像进行拟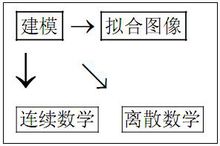合。

建模

图像复原模型可以用连续数学和离散数学处理，处理项的实现可在空间域卷积，或在频域相乘。

图像复原的基本任务:消除模糊。

图像退化成像系统受各种因素的影响，导致了图像质量的降低，称之为图像退化。

因素包括:传感器噪声、摄像机聚焦不佳、物体与摄像机之间的相对移动、随机大气湍流、光学系统的象差、成像光源和射线的散射等。

退化基本表现：图像模糊1。

数学模型从上面对图像复原技术的概述我们可以看到，图像复原技术的基础应该是图像退化的数学模型，不同成像系统具有的图像退化模型是不相同的。

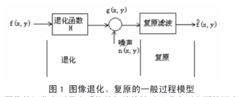
图像的退化主要是由系统的相关特性以及噪声两方面的因素所导致的，我们可以通过设计一个合适的复原滤波器（即实现逆滤波过程）来实现图像的复原。图1 中f（x，y）表示的是一幅静止、二维的图像，它在外部噪声n（x，y）的干扰作用之下，在经过系统h（x，y）之后，退化成为g（x，y），复原后的图像为f（x，y）。针对于退化图像的复原，我们通常可以采用这样两种方式来进行：其一，当对于原始图像缺乏必需的先验知识时，我们可以采用就退化过程建立一个模型，首先对其进行一个大概的描述，然后在复原的过程根据具体的情况进行逐步合理的修正，逐步消除误差影响。这种方法建立在对图像的退化过程进行合理的估计的基础之上，从这个角度来看它是一种估计的方法；其二，当我们对原始图像具有足够的先验知识时，我们这时候则直接针对原始图像建立一个精确的数学模型，然后再对退化图像进行复原处理，这种效果更好2。

噪声处理（一）图像噪声的分类。我们通常将影响图像质量的噪声分为这样四种基本的类型：其一，那些记录于感光胶片中的图像容易受到感光颗粒噪声波动的影响；其二，当图像从光学形式向电子形式进行转换的过程中，它是以一个统计的形式进行的，这主要是由于每个像素所接收到的光子的数目是随机的，而且是有限的，这样就导致了光电子噪声的产生；其三，电子放大器在对信号进行处理的过程中还会引入热噪声；其四，在获取图像的过程中，容易从电力或者是机电干扰中获取周期性的噪声。

（二）根据图像的特征建立起相应的概率密度函数。在对数字图像进行处理的过程中，一般需要以概率密度函数作为根本的依据来对噪声的统计特性进行表述，建立起对应的数据模型。常见的几种典型噪声主要包括：高斯噪声；锐利噪声；伽马噪声；指数分布噪声；均匀分布噪声以及脉冲噪声六种。由于篇幅所限，这里不再对各种噪声的概率密度函数进行介绍。

（三）对噪声的相关参数进行估计。在对噪声进行处理的过程中需要获得各种噪声的相关参数，这是掌握图像先验指数的一部分。例如，在用维纳滤波（即最小均方）的方法对图像进行复原处理，采用卡尔曼滤波对图像进行平滑处理、边缘检测以及图像的分割等操作等，都需要对噪声的方差进行估计。在通常的情况下，由于所拥有的主要资料就是已经退化了的图像，这是只能对噪声方差进行盲估计。噪声方差的估计主要包括这样两种：其一，首先对噪声的图像进行预滤波处理，然后再对经过滤波处理后的数据进行方差估计处理；其二，在估计前将噪声分成多个区域，主要针对其中的“平坦区”对噪声方差进行估计。通常所采用的估计方法有：平均法、中值法、分块法，散点法，金字塔法以及预滤波法等几种。

（四）去除噪声。去除噪声的一个基本理论就是根据噪声的高频特性来提出低通滤波的方法，常用的去除方法有均值滤波法以及中值滤波法等。这两种方法虽然能去除噪声，但是也去除了图像的相关细节，导致图像的边界模糊。因此，现在一种基于模型的去噪算法被提出，该算法主要是基于图像本身的马尔可夫模型及不同噪声而提出来的。