提出赫兹1882年发表了关于接触力学的著名文章“关于 弹性固体的接触(On the contact of elastic solids)”,赫兹进行这方面研究的初衷是为了理解外力如何导致材料光学性质的改变。1
弹性固体的接触(On the contact of elastic solids)”,赫兹进行这方面研究的初衷是为了理解外力如何导致材料光学性质的改变。1
为了发展他的理论,赫兹用一个玻璃球放置在一个棱镜上,他首先观察到这个系统形成了椭圆形的牛顿环,以此实验观察,赫兹假设玻璃球对棱镜施加的压力也为椭圆分布。随后他根据压力分布计算了玻璃球导致的棱镜的位移并反算出牛顿环,以此再和实验观察对比以检验理论的正确性。最后赫兹得到了接触应力和法向加载力,接触体的曲率半径,以及弹性模量之间的关系。赫兹的方程是研究疲劳,摩擦以及任何有接触体之间相互作用的基本方程。
介绍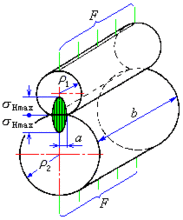
由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现于节点附近。因此,通常计算节点的接触疲劳强度。如图表示一对渐开线直齿圆柱齿轮在节点接触的情况。为了简化计算,用一对轴线平行的圆柱体代替它,两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径。由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为
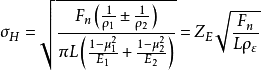
式中 :接触应力(Mpa)
:接触应力(Mpa)
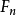 :法向力(N)
:法向力(N)
L:接触线长度(mm)
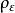 :综合曲率半径(mm),
:综合曲率半径(mm),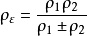 ;
;
±:正号用于外接触,负号用于内接触
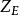 :材料弹性系数,
:材料弹性系数,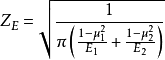 ,其中
,其中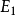 、
、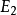 分别为两圆柱体材料的弹性模量(MPa);
分别为两圆柱体材料的弹性模量(MPa);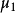 、
、 分别为两圆柱体材料的泊松比。
分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大。但为了简化计算,通常控制节点处的接触应力。2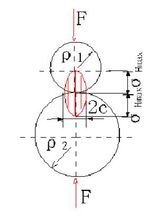
两圆柱体接触时,接触面半宽a为:
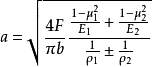
两球体接触时,接触面半径c为:
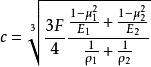





 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国