单个科学家不可靠，整个科学界能可信吗？丨展卷

在法国高中课程里，贝叶斯公式是一个简明扼要的数学定理，是一个紧凑的等式。其证明只需要一行，而且只需要用到乘除法和有关概率的概念。比起要求高中生和大学生掌握的许多其他数学概念来说，这个公式似乎远远更容易学会。但是，即便是最好的数学家也未必理解这个公式。贝叶斯公式的深邃，远远超乎了我们的想象。

本文经授权转载自《贝叶斯的博弈》（人民邮电出版社2021年2月第一版），标题为编辑所加，有删节。前往“返朴”，点击“在看”并发表您的感想至留言区，截至3月18日24点我们会选出2条留言，每人赠书一本。

撰文 | [法]黄黎原（Lê Nguyên Hoang）

翻译 | 方弦

初始的力量被注入数种甚至一种生命形态之中，即使这个星球一直按照引力决定的法则周而复始地运动，但从如此简单的起点出发，却演化出了众多无限美好而神奇的生命形式，并将继续演化下去。这种对生命的视点无比壮丽。

——查尔斯·达尔文（1809—1882）

幸存者偏差

在第二次世界大战中，英国空军雇用了统计学家亚伯拉罕·瓦尔德研究战机装甲的最优化。英国空军注意到，除了前部发动机所在之处以外，从战斗中返回的战机被打得遍体鳞伤。于是空军得出结论，应该减轻前部装甲来强化后部装甲。瓦尔德惊呼：这不对！他的看法是，事情正好相反，飞机只有后部中弹证明了应该加强飞机的前部装甲。

瓦尔德的这个说法相当惊人。但这其实本质上类似于查尔斯·达尔文对生物中复杂结构的出现做出的解释。在这两种情况下，我们当中大部分人所忽略的微妙之处正是淘汰的过程，或者说，我们注意的只是选择中的幸存者。在瓦尔德的情况中，被淘汰的就是那些前部中弹的飞机，这些飞机的发动机被摧毁甚至爆炸，因此无法返航。与之相似的是，达尔文断言那些因缺陷而无法繁衍的动物物种不可避免走向灭亡，因此，在至今仍然存活的物种中，重大缺陷极少。

达尔文的演化理论受到了科学界的一致赞赏，但时至今日，它仍有许多伪科学的批评者。智能设计论证正是这些人用以反驳的工具，这项论证如下。想象一下你在沙漠的正中，如果你偶然发现一块奇形怪状的石头，那么你不会惊奇于它是自然过程的产物。然而，如果你发现了一块结构精巧的钟表，那么认为它可以通过完全自然的过程产生，似乎太愚蠢了。钟表的精巧结构似乎只能用有一位拥有智慧的设计师精心制作来解释。同样，人体那令人惊叹的精巧结构，从骨骼与肌肉的生物力学，到免疫系统的组织，再到灵巧的眼睛以及复杂得难以理解的大脑，都只能是智能设计的结果，而这位拥有智慧的设计者只能是上帝。

这个论证可能看上去很有说服力。然而，除了其中将“拥有智慧的设计者”与上帝混为一谈这一点值得商榷以外，它也低估了我们上文所说的淘汰过程——达尔文将其称为自然选择。

加利福尼亚的五彩蜥蜴

我们现在来到美国加利福尼亚州的中央谷地，那里生活着三种不同的雄性蜥蜴，粗略来说，它们是橙色蜥蜴、蓝色蜥蜴和黄色蜥蜴。这些雄性蜥蜴属于同一物种，所以它们会寻求与同一种雌性蜥蜴进行繁殖。但它们在繁殖上拥有截然不同的特性和策略：橙色蜥蜴非常粗暴，它们控制着特定的领地，并且与自己领地中的所有雌性交配；蓝色蜥蜴是忌妒心很重的“一夫一妻制”实行者，它们会控制伴侣的一举一动；最后，黄色蜥蜴是那种偷偷摸摸的花花公子，只要碰到雌性就飞扑上去。

达尔文的演化理论指出，最有能力繁衍的蜥蜴就是能够存续的那些蜥蜴。然而有趣的是，不同雄性蜥蜴的繁殖能力取决于当前其他的雄性蜥蜴种群。

举个例子，假设大部分雄性蜥蜴是粗暴的橙色蜥蜴。这样的话，每只橙色蜥蜴都会占据一个庞大的“后宫”，从而无法很好地监视雌性蜥蜴。这时，偷偷摸摸的黄色蜥蜴很容易就能与那些未被监视的雌性蜥蜴“幽会”，这样的话，雌性蜥蜴因偷偷摸摸的黄色蜥蜴受精的可能性比因粗暴的橙色蜥蜴受精的可能性高。我们预期偷偷摸摸的黄色蜥蜴的数量会逐渐超过粗暴的橙色蜥蜴。

现在想象一下，占主流的是偷偷摸摸的黄色蜥蜴。那么嫉妒的蓝色蜥蜴就可以诱惑雌性并据为己有，这样的话，所有雌性蜥蜴就会逐步与蓝色蜥蜴结合。因此，偷偷摸摸的黄色蜥蜴就无法找到名花无主的雌性蜥蜴，从而无法繁衍。于是嫉妒的蓝色蜥蜴就会导致偷偷摸摸的黄色蜥蜴灭绝。

最后，我们假设绝大部分雄性蜥蜴是嫉妒的蓝色蜥蜴。这样的话，粗暴的橙色蜥蜴就会与这些嫉妒的蓝色蜥蜴争斗，将雌性蜥蜴一个一个地扩充进自己的“后宫”。这些嫉妒的蓝色蜥蜴就都会变成单身，也无法繁衍。它们最后就会消失，而获益的是那些粗暴的橙色蜥蜴。

总结一下，大体来说，橙色会输给黄色，黄色会输给蓝色，而蓝色会输给橙色。这跟“石头、剪刀、布”很相似，石头能打败剪刀，剪刀能打败布，而布能打败石头。这个博弈拥有唯一的纳什均衡，就是随机选择这三个选项。这也在意料之中。人们在现实中观察到这三种雄性蜥蜴在自然环境下共同存在，就像是它们根据“石头、剪刀、布”的纳什均衡进行了选择一样！也就是说，虽然纳什均衡这个概念本来只能由拥有智慧的参与者实施，但它似乎也完全可以应用到达尔文式演化的结果上。我们会看到这并非偶然。

洛特卡 - 沃尔泰拉动力学

生物学家约翰·梅纳德·史密斯在 1972 年提出了演化稳定策略这一概念。史密斯将这种策略定义为种群的特定构成，在遭受构成不同的（相对较小的）外来种群入侵时（比如投放 100 只黄色雄性蜥蜴）也能维持稳定。在现实中，这一般对应着种群由于统计涨落产生的随机变化。这种统计涨落是否会对种群产生深远影响？或者说，达尔文式演化是否会将种群的构成重新引向统计涨落出现之前的状态？

为了回答这些问题，我们将会深入、细致地探索达尔文式演化的一个简化模型。“所有模型都是错的”，但我们将要谈到的模型对于众多生物学家来说相当有用。

你猜到了吗？支配演化的方程不过是伪装之后的贝叶斯公式！实在难以置信！与主观概率对应的是比例zi。从t变为t+1时，这些概率会依据某种贝叶斯推断过程产生变化，其中的思想实验项由1+fitnessi代替。最后，分母是配分函数，可以保证zi的和在t+1时仍然为 1。

这就是经过分析后令人目瞪口呆的结果。如果将时刻t的适应度看作理论i解释直到时刻t所得到数据的能力，那么达尔文式演化与理性客体毫无二致！

这种比较也许看似荒谬，却有另一引人注目的定理作为佐证（即使它在数学上是显然的）。这个定理由生物学家约翰·梅纳德·史密斯在 1973 年证明，它断言达尔文式演化产生的种群变种比例必然属于纳什均衡。惊人的是，这些纳什均衡对应着拥有智慧的理性客体在博弈中采取的策略。换句话说，正如沙漠中的钟表一样，纳什均衡所刻画的比例分配似乎只能是出于智慧客体的某种意图的结果，至少人们会有这种朴素的信念。但事实并非如此。

看似是智慧的果实，却只是达尔文式演化不可避免的结果。这就是梅纳德·史密斯的这一定理令人瞠目结舌的结论。

遗传算法

达尔文式演化远远不止是人类智慧苍白的复制品，实际上它能轻易创造出人类智慧也难以想象的结构——常被引用的经典例子就是人类大脑。虽然演化知道怎么将它设计出来，但即使有了超级计算机，神经科学到现在还无法完全理解人类大脑。

来自达尔文式演化的这种精巧复杂如此摄人心魄，令计算机科学家与应用数学家转向了所谓的遗传算法，用以找出某些问题的答案，而除此以外的解法无人知晓。这些遗传算法除了模仿自然选择，还模仿了杂交与变异。

比如说，假设我们希望确定一个访问法国最大的 100 个城市的方法，使得路程费时最少。这个问题又叫作旅行推销员问题。每个访问城市的顺序都是问题的可能解答，而我们的目标是找出最优的解答。这个问题的难点在于可能的解答有如恒河沙数，一共有100!≈10^157个可能的路线。即使我们将地球上所有超级计算机组合起来，列出所有排列，完成这一任务所需的时间也远远超过了宇宙的年龄。

遗传算法对于这类问题的处理无比高效。这种算法的原则就是维持一个多样化的种群，其中包含有前途但并非最优的解答。在每一步迭代时，算法会选择种群中的两个解答，对其进行杂交操作，在其中添加（有益的）变异，然后进行选择，其中最差的解答会被淘汰。奇怪的是，这种达尔文式的优化方法好得惊人，甚至是许多情况下最优秀的解法！

达尔文式演化在这种情境下比人类的智慧要做得更好。所以，自然的精巧作为反驳演化理论的论点并不令人信服。但我们在第 11 章仍然会谈到这个问题。

构筑自己的意见？

科学与伪科学之间的区别，是被称为“怀疑主义”“批判性思考”或者“探索派”的思想运动偏好的话题。这一思想运动主要讨论伪科学支持者的常见诡辩与认知偏差。这些论证中的错误的确相当糟糕，是大量阴谋论、替代医学和超常现象的基础。

对于某些人来说，对这些问题的正确反应是构筑自己的意见。然而，这种反应的危险在于，有些事情必须具有大量知识或者经验储备才能得出足够切中要害的意见，但这种反应难免导致对这些事情的怀疑，甚至是无法避免的偏见、误解和错误。例如琳达问题、 值争议或者差分隐私的概念就属于这一类情况。某些更重要的问题，比如疫苗的有效性、谷歌和 Facebook 的算法，以及气候变化的人为因素，也都属于这类情况。除非你花上好几年细细研究这些问题，否则你自己形成的意见必定缺乏足够的信息，也因此无足轻重。

我们十分希望即使只花上几个小时，最终也能在这些问题上得出正确的答案，但事实远非如此。比如说在琳达问题中，直觉会使我们的错误率比一只随机选择答案的黑猩猩的错误率还要高。统计学家汉斯·罗斯林就证明了这一点。对于许多问题，比如女性平均受教育时间、自然灾害造成的死亡人数、世界贫困人口等，我们的表现比无知还要糟糕，我们一贯选择的都是错误答案！

更糟糕的是，要估计应该对自己的直觉有多少信心，对我们来说难上加难。因此，即使花上相当长的时间思考并汲取有关某个问题的信息，我们对于自己理解了多少，以及自己的意见是否考虑了足够多的信息，了解起来可能还是相当困难的。雪上加霜的是，德里克·穆勒的博士论文证明，哪怕是对物理现象完全正确的视频解释，也可能会提高学生对自身直觉的信赖，即使学生刚才观看的视频解释完全否定了这些直觉！

我们每个人都经历过太多次这种反复出现的自信过度了。你可能也明白，这就是我在本书中尝试克服的主要认知偏差。这也是贝叶斯公式、埃尔德什在蒙蒂·霍尔问题中遇到的困难，以及所罗门诺夫不完备性迫使我们承认的东西：我们总是过分自信。正如伟大的逻辑学家伯特兰·罗素所言：“世界上所有问题的根源在于，笨蛋和盲信者总是无比自信，而更有智慧的人却一直在怀疑。”艾蒂安·克莱因 **（注：法国的物理学家及科学哲学家）**补充道：“要尽量避免得出结论。”

实际上，“只靠自己”去相信任何事物是个难于登天的任务，其中布满无法逾越的障碍。我很不建议你这样做。如果构筑正确的意见那么容易的话，那高等研究就不需要花那么长的时间了，而且知识也不会被如此切分为相互隔绝的学科了。如果没有足够的财力、时间和认知能力去沉浸在特定问题的详细研究之中的话，那么我们就难免需要依靠他人的意见。这并不是个坏习惯。实用贝叶斯主义者也更倾向于利用其他人在数十年甚至数百年中做出的工作来细化自身对世界的理解。即使是纯粹贝叶斯主义者也知道，其他个体能访问众多她无法访问的数据，所以她有不少东西可以向这些人学习。

单个科学家并不可靠

所以，要理解我们身处的这个世界，诉诸权威是一个强大、有效且实用的工具。然而这也带来了下面的问题：谁是最可靠的权威？爱因斯坦提出的论证是否比莎士比亚的论证更有价值或者更值得相信？我们可不可以盲目信任科学家？

在面对这些问题时，某些探索派学者（也就是捍卫批判性思维的人）和某些科学家会强调科学方法的客观性。他们认为，科学家得出结论的方法就是完全严谨、客观并且经过同行评议的论证。因此，他们的结论比伪科学家的结论更有价值，因为伪科学家并不遵循这一方法。

然而，优秀的探索派学者会提防这种粗糙而刻板的论证。首先，某些伪科学或多或少遵循的是科学方法的路线。此外，贝叶斯主义否定了这种科学方法的客观性，甚至也否定了它的正确性！但更重要的是，科学工作者几乎从来不按照科学方法做事。

在科学文献中任意选取一篇论文，论文的作者很有可能并没有提出什么假设，也没有确定某个带有限制的实验流程，同样没有根据这个流程来进行实验，最后也没有用 值得出结论、完成论文。无论是现代还是过去，科学更像是一连串的试错、建模、模拟、参数调整，以及实验中的质疑。通常只有在获得所有结果之后，论文的写作才开始。写作时，作者选取的角度通常忽略了实验室中绝大多数错误线索，为的是更好地将新发现组织起来，并推出一个引人深思的结论——大部分读者也觉得这相当值得赞赏。

更糟糕的是，科学工作者同样无法避免那些导致伪科学的认知偏差甚至诡辩的荼毒。这是因为，正如我们在第 1 章和第 2 章中看到的那样，即使是最优秀的科学工作者，面对某些简单却令人困惑的问题也无能为力，就像埃尔德什在面对蒙蒂·霍尔问题时那样。曾经有很长的一段时期，最优秀的科学家认为地球是宇宙的中心、几何必须是欧几里得几何，或者人工神经网络是人工智能研究的死胡同——当我在 2011 年第一次看到人工神经网络的数学描述时，我的反应就是这样的！

即使是伟大的爱因斯坦，做出过对于许多物理学家来说如同奇迹的突破，他也曾经反复犯下错误，比如在 1913 年为有问题的广义相对论前身做辩护，还有为了强行加入稳态永恒宇宙的可能性而在广义相对论方程中引入了一个宇宙学常数——他自己将其称为“一生中最大的错误”。无论是现在还是将来，即使像最优秀的科学家那么聪明的人，拥有的认知能力也有极限。

还有更严重的问题。学术界体系中的一些激励措施与对认知偏差的永恒斗争并不相容。这是因为，某个科学工作者的声誉，或者仅仅是保留当前职位的能力，依赖于其思想的独创性和发表论文的数目。在这种情况下，科学工作者有着充足的动机去疯狂捍卫自己的思想，而且通常超出了贝叶斯公式允许的范围。科学工作者甚至有动机去杜绝贬损自己过去提出的并曾给自己带来荣誉的理论，即使这些理论最终被否定了。最后，科学工作者却没有动机去花时间验证与其竞争的理论的正确性，因为科学期刊不会发表对已有理论的巩固工作。

最后，在某些极端但确实存在的情况中，某些科学工作者的科研经费来源要求他们得出某些预定的结论，比如说那位向烟草产业出卖了灵魂的罗纳德·费希尔。然而，我们也无法完全排除这些不正常的经费来源。

这几个论点似乎伤害了科学工作者的可信度。此外，当我看到某些著名科学家在公开演讲中使用某些论证捷径时，我对他们的言论的置信度就遭到了沉重打击。从我自己的角度来说，在为 Science4All 或 ZettaBytes 制作视频时，我倾向于极度回避技术难点，从而传递出令人信服而且饶有趣味的清晰信息，因为这些视频的首要目的是推广数学和计算机科学。正是出于这个原因，我曾多次向受众说谎——包括在这本书中。我深深仰慕的其他科学家在我之前也说过这种有意的谎言，但这一点都不出人意料。在介绍哥德尔的定理时却没有介绍一阶逻辑的那些人，必定也要说一点小小的谎言。力图面向一般大众推广科学会迫使我们在措辞中更偏好流畅，而非严谨。

诉诸权威

话虽如此，某些专家在某些特定问题上的意见对我来说有着完全不同的价值。我在预科班第一年时的数学老师就是这种情况。跟很多学生一样，我对他那些意见的重要性心悦诚服。如果我们的想法在某个数学问题上有冲突的话，我不仅会立马开始强烈怀疑自己，甚至还会完全否定自己的信念。但更重要的是，我很快就会相信他的想法，并尝试理解这些想法的根源。

同样，如果某位著名科学家多次令我震惊于其见解中的智慧，那么当他针对其专门领域的特定问题说出惊人的意见时，无论我在听到这个意见之前相信的是什么，我对这位科学家表达的意见的置信度都会急速上升。

举一个例子。某位研究逻辑的朋友有一次跟我说，跟粗糙的论证以及维基百科上写的正好相反，存在这样的数学模型，其中所有实数都是可定义的。我曾多次见识过他在数理逻辑方面的造诣，即使我对维基百科的数学页面有着很高的置信度，我还是开始严重怀疑我此前的想法，甚至很快就相信了我朋友的说法，即使我并不明白为什么他会相信有这么一回事。

这就解释了为什么纯粹贝叶斯主义者会无视那些权威气候怀疑论者。石油企业有着巨大的经济效益，它们能找到愿意捍卫其观点的人，这一点毫不令人意外。除此之外还有巨大的选择性偏差。如果某个节目愿意给气候怀疑论者提供发声的渠道，那么受邀者捍卫气候怀疑论的概率必然等于 1，即使他的论点是错误的。

尽管如此，这个论证对于对立阵营同样有效。即使气候变暖是错误的，某位激进环保主义者为气候变暖辩护的概率仍然接近于 1。如果激进环保主义者可以这样说的话，那么那些被邀请到媒体上露面的科学工作者也可以这样说，这出于我们在上面说过的那些认知偏差，而科学工作者也是这些偏差的受害者。一言以蔽之，对于类似气候变暖这样牵涉重大经济或政治利益的富有争议甚至引起意见两极分化的问题，诉诸权威的论证几乎毫无效果。

所以，有时候我相信某些自己没有理解的事情。甚至可以说，我之所以相信这些事情，都是因为诉诸权威的论证。有些人断言这不是理性的。然而，即使我当下不知道这些事情是否正确，这事实上也是唯一理性的后验立场——至少在相信贝叶斯公式的情况下 。

科学共识

我们回到气候变化的问题。我们已经看到，任何一位科学工作者都不能作为权威。此外，与其挑出某位气候学的专家，探索派学者通常更重视气候学界的意见。然而意见只有一个，气候学界的绝大部分工作者相信气候在变化，而且这种变化来源于人类——在报道中，这个群体中这样认为的人数通常超过 98%。但如果每一位科学工作者都不可信的话，为什么整个学界的意见就更为可信呢？

对于这个问题，纯粹贝叶斯主义者有一个重要的答案：与每个成员相比，科学共同体对贝叶斯公式的应用更恰当。如果将科学共同体想象成一块土地，那么不同的理论T则是在这块土地上生活着的不同物种的动物。在每个时刻t，最令人信服的理论更能繁衍下去。这些理论更容易被科学工作者所接受。我们将在时刻t接受某个理论T的科学工作者的比例记作PT(t)，洛特卡–沃尔泰拉方程就能应用到思想的演化上 (为了方便，不失一般性，我将 fitness + 1 换成了 fitness) ：

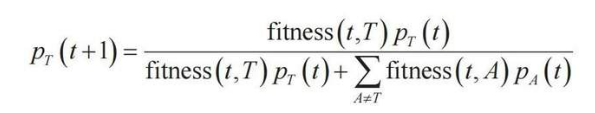
你明白我要说什么了吗？不同理论在科学共同体中的达尔文式演化，正是伪装过的贝叶斯推断！

换句话说，这就像是科学共同体应用了贝叶斯公式来使最可信的理论脱颖而出。正因如此，科学共同体理应拥有的置信度要远远超越其中任何个体的意见。只要理论的适应度与思想实验项相关，那么科学共同体就比其中任何个体都更能贴切地应用贝叶斯公式。

作者/译者简介

黄黎原（Lê Nguyên Hoang）：瑞士洛桑联邦理工学院科学信息与通信学院研究员，美国麻省理工学院博士后，加拿大蒙特利尔理工学校应用数学博士。设立多个科普网站、网络视频频道及播客，著有多部数学、计算机理论著作。

方弦：巴黎七大组合数学博士，曾于波尔多、里昂、格拉茨等地大学工作，现为巴黎居斯塔夫·埃菲尔大学计算机系助理教授。