什么是一个好模型？预测与解释重要得多

民间一直流传这样一句俗语：“穷人算命、富人看风水”。

意思是，算命的人会根据自己的命运，把握最佳的时机，使自己发挥出命运的最好状态，会在原有的基础上提升自己的财富。看风水的人，则是避免可能对运势产生影响的不利因素，在原有的基础上锦上添花。

这两者都不外乎一个词：预测。

人们对预测事物的发展非常热衷，但往往对“事后诸葛亮”（解释）不屑一顾。

一次让高斯声名鹊起的预测

1801年年初，天文学家朱塞普·皮亚齐（Giuseppe Piazzi）发现了一颗不在星表上的星星，后将其命名为谷神星。皮亚齐跟踪了这颗星星40天，并且记录了相关的数据。可是之后由于地球的轨道运动，谷神星消失在太阳耀眼的背景眩光中。虽然再过几个月，谷神星脱离了太阳背景眩光，应该可以被重新观测到，但是这要求我们知道谷神星的轨迹。然而，因为40天的观测数据较少，当时的数学工具还无法根据这些数据准确计算或预测出谷神星的轨道。

在当时，计算太阳系内的某个行星绕太阳运动的轨道还是一个难题。因为我们是在地球上进行观测的，在行星运动的同时，观测点地球也在运动。并且地球和行星的运动轨道不在一个平面上。

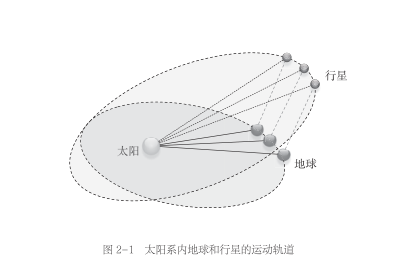
天文学家们观测到的、可以用于估计图中行星运动轨道的信息，只包括每次观测时地球的位置和当时从地球到行星的观测角度。

这时，卡尔·弗里德里希·高斯（Carl Friedrich Gauss）出现了。

高斯当时只有24岁，虽然年轻，但他研究包括月球的运动等与天体运动相关的问题已经有很多年。他18岁在计算天体运动轨道时，就发明了最小二乘估计这一方法。高斯拿到皮亚齐的观测数据后立刻开始计算谷神星的运动轨道。在计算轨道时，高斯除了借助最小二乘估计来消除观测误差，还发明了一系列方法来提高对行星运动轨道的估计精度。

很有意思的是，高斯在计算完成后，在11月底把他预测谷神星运动轨道的结果发给了他的一个朋友，匈牙利天文学家弗兰茨·萨韦尔·冯·扎克（Franz Xaver von Zach）。冯·扎克收集了高斯、他自己和其他一些人的预测结果，并把这些结果发表在1801年12月初的一本天文学刊物上。值得一提的是，高斯的预测结果和其他人的有很大不同。

然而，如同真理掌握在少数人的手里那样，只有高斯准确预测出谷神星的位置：在1801年12月31日，谷神星消失在人们视线中一年后，冯·扎克在高斯预测的位置附近重新找到了谷神星！两天之后，天文学家海因里希·奥伯斯（Heinrich Olbers）也根据高斯的预测结果发现了谷神星。

这个成就让当时年仅 24 岁的高斯在欧洲天文学界一下子声名鹊起。高斯在1809年将最小二乘估计的公式发表在被后世奉为圭臬的巨著《天体运动论》中。

高斯靠计算模型推演出谷神星的运行轨道，从而成功预测出谷神星的位置。

一个好模型应该是怎样的

我们先来看下面这张图。这张图统计了某公司过去几年的利润情况。图上有6个点，每个点都分别对应一年的利润。

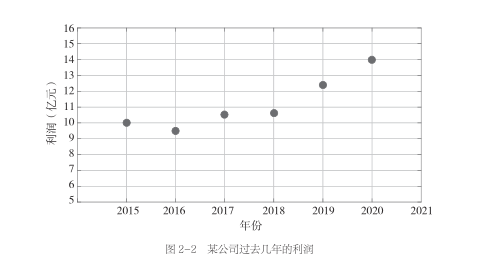
我们能够看到这家公司的利润变化趋势：前4年保持稳定，后2年开始有所增长。

现在，如果我们想要根据这6个点预测这家公司未来两年的利润，应该怎么办呢？你需要根据现有的这6个点画出一条曲线，然后再把这条曲线按照过去的趋势延伸到后几年。有一个专业的词汇用于形容找到这条曲线的过程，叫作“曲线拟合”。

曲线拟合通常分为两步：首先确定曲线的基本形式，然后找到该形式下的最优参数。我们通常可以自己选择曲线的形式，而最常用的莫过于多项式形式。

对于上面这个例子，如果我们假设有时间t，而利润y是时间t的函数，那么一阶多项式的形式为：y = a + bt

图 2-3 显示了我们用最小二乘估计得到的最优系数所对应的直线。

我们可以看出，虽然这条直线大致反映了利润变化趋势，但是这些已有数据点并没有都和这条直线重叠，有些点与直线的差距还比较大。这条直线“解释”已有数据点的能力并不算太强。

我们来看看如果我们选择二阶多项式来拟合这些点会发生什么。

在这个例子中，二阶多项式反映的利润不仅和时间有关，也和时间的平方有关：

y = a + bt + ct2

我们通过观察可以发现，已有数据点都比较接近这条曲线。而且很有意思的是，这条曲线还反映了企业最近几年加速增长的趋势。

和之前的那条直线相比，总体上图2-4中的这条曲线更好地反映了已有数据点。

如果再仔细看一下图 2-4，你会发现仍然有一些点不在这条曲线上。要想让这 6 个点都在这条曲线上，我们需要五阶多项式（见图2-5）。

图2-5上的这条曲线经过了每一个已有数据点，这是之前的直线和曲线都做不到的。也就是说，这条曲线的解释能力比之前两条线更强，它达到了一个极致，能够完美地解释所有已有数据点。从解释能力上来看，五阶多项式肯定是最好的，但它一定是最好的模型吗？

肯定不是。

这个模型的意义在于预测这个公司之后几年的利润。如果用这个五阶多项式进行计算，我们可以发现，这个公司之后几年的利润会急剧下降，这显然预测得不够合理。

为什么会出现这一现象？机器学习中的“过度拟合”一词可以解释。过度拟合，是指这个模型可以很好地解释已有的数据，但是对没见过的数据预测得很差。

我们很容易发现，想使一条曲线具有好的解释能力其实很容易，但是，想使一条曲线具有好的预测能力则不是一件简单的事。

现在，我们应该可以回答“一个好模型应该是怎样的”这一问题了。

一个模型对未知数据的预测能力是判断其好坏的唯一标准。

想判断一个模型的好坏，关键要看它对未知事物的预测能力，而不是对已知事物的解释能力。每个人都可以找出很多理论来“解释”已知，但是只有正确的理论，才能准确“预测”未知。

简单来说，解释价值不高又很容易；预测很珍贵，但又真的很难。所以，未雨绸缪永远比“事后诸葛亮”更让人信服。

文章由科普中国-星空计划（创作培育）出品，转载请注明来源。

作者：北京航空航天大学副教授、博士生导师 刘雪峰

审核：华中师范大学数学与统计学学院 副教授 邓清泉