模拟退火算法：为什么年轻时应该多去闯闯？

互联网上经常会出现相互矛盾的词。从十几年前开始，“逃离北上广”就反复被年轻人提起。很多年轻人因为大城市房价高、压力大，选择回家乡小城市过安逸日子的案例屡见不鲜。和“逃离北上广”相反，最近有个新词叫“回笼漂”，形容的是很多离开北上广深等一线城市回到家乡的年轻人，又返回一线城市工作和生活，比如“回笼北漂”、“回笼杭漂”等。

那么，在“逃离北上广”和“回笼漂”这两个不同的选择之间，到底应该如何选择呢？这个问题对于年轻人尤其重要。经常有学生问我这样一个问题：毕业之后，是回自己的家乡还是去大城市闯一闯？是找一个自己有激情的方向创业还是选择一个稳定的工作？

图片来源：图虫创意

我今天想通过计算机领域著名的“模拟退火算法”来给出答案。

什么是“模拟退火算法”

20世纪70年代末至80年代初，IBM沃森实验室的两位科学家斯柯特·柯克帕特里克（Scott Kirkpatrick）和C.D. 格拉特（C.D.Gelatt）在研究优化算法时，从物理学中得到了启发，发明了模拟退火算法。

我们先说说退火。

大家从电视剧或电影上应该都看到过这样的情节：铸剑师在炉火中反复敲打一个烧得很红的剑胚，火星四溅。完成敲打之后把剑放进水里，只听见“呲”的一声，升起一阵白雾，然后铸剑师再磨一磨剑的表面，就有了一把削金断玉的宝剑。

将宝剑丢入水中是一种金属加工环节的冷却工艺，被称为“淬火”。淬火过程中金属会在液体中快速冷却，内部结构会发生改变，具体来说就是会变得很硬。

淬火应该是一种大家最熟悉的冷却工艺。除了“淬火”还有一种冷却工艺，就是退火。

退火的冷却速度比淬火慢得多。退火通过缓慢降低金属的温度，使金属内部组织达到或接近平衡状态，帮助金属内部释放应力、增加材料的延展性和韧性、产生特殊的显微结构等，从而获得良好的工艺性能和使用性能。

柯克帕特里克对于退火有一个洞见，他解释道，在退火过程中，材料冷却的速度会对其内部结构产生很大的影响。而在物理学中，“温度”和“随机性”是对应的：温度越高，随机性越强。

退火的过程，代表随机性从高到低的衰减。

模拟退火算法的三种求解方法

模拟退火算法是解决函数优化问题的数值解法，我们先从找到函数的极值说起。例如，如果让你找到函数 y = -x2 + 2x 的极值，你会怎么做？

有三种方法可以完成求解。

解法1：解析解

大家最熟悉的解法是对函数的表达式求导，令导数为0。这个方程的解就是这个函数的极值。

上面这个函数的导数形式为：yʹ = -2x + 2

令导数为 0，即：-2x + 2 = 0

表达式中x = 1，这就是使该函数得到极值的解。用这种方法得到的值，叫作该问题的解析解。

解析解一定是最优的，但是要找到解析解通常不那么容易。实际应用中很多函数的导数形式十分复杂，甚至函数本身不可导。

解法2：梯度法

梯度法的核心思想就是“找准方向，精益求精”。

我们用图16-1来解释这个思想，图16-1中的曲线，就是这个函数y的表达式的图像，我们想找到这个函数最大值对应的x的位置（灰点处）。

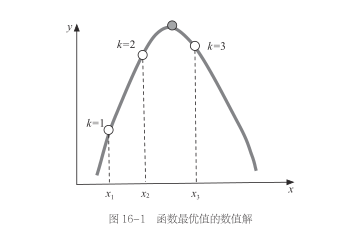
第一步（k = 1）：随便猜一个x值。假设我猜的位置为x1（见图16-1），当我们猜到x1这个位置以后，判断下一步的方向，极值是在x1的左边还是右边？

这里就要用到梯度了。梯度就是函数的导数，在这个例子中，就是斜率。x1处的斜率是正数，这意味着增大x的值会让y值上升。

接下来，我们将x往右移一点，可以得到更大的y；然后根据梯度法的原则，继续右移x……不断重复上面的步骤，我们就可以逼近最优的灰点的位置。

解法3：爬山法

爬山法的思想和一个人爬山的过程很相似。一个人在爬一座陌生的山时，只需要时刻保证自己现在的位置比前一刻高，最后就可以爬到山顶。

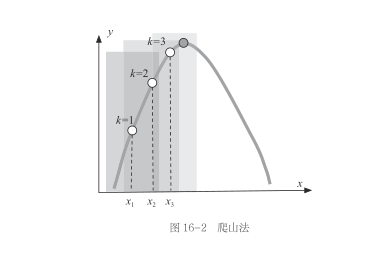
就算法而言，每次从当前的变量x附近，选择一个对应的函数值y比现在的变量x更高的位置作为下一步的x。不断按照这种方式调整，，直到y收敛为止。直到到达某一个x，这个x附近的点对应的y都比该x对应的y要小，这样就找到了最高点的位置（见图16-2）。

爬山法有一个很大的问题，就是找到的位置很可能是一个局部。极大值（该点比周围的点都要大，但是比远处的很多点要小）。试想一下，如果你在大雾天爬山时视野有限，那么按照爬山法，你很可能最后到达的只是一个小山坡（局部极大值）。虽然小山坡比其周围的位置都高，但其距离真正的山顶（全局极大值）还差得很远。

图16-3就是这样的一个例子。从图中的初始起点出发，按照上面的爬山法的原则不断调整，最后就会到达图中的局部最高点，而无法到达远处的全局最高点。

为什么会出现这种现象？首先是因为这条曲线比较复杂（有多个高点）。其次，上面的算法中，每次都是在当前x的基础上进行小幅调整，并且要求每一步调整后的x对应的函数值换都要比调整前的要高。这样的话，如果某一次达到了局部最高点，那么算法就会发现x对应的函数值已经比x周围的点都要高，那么就停了下来。

要到达远方的全局高点，需要从局部最高点往下走，翻过这个山谷，然后才能爬上全局最高点。因此我们看出，句话说，这些数值解法之所以会陷入局部极大值最高点无法跳出，是因为算法总是要求下一步的结果比上一步好，这就导致算法无法翻过这个低谷，从而迈上右侧的高峰。它们

对于一个人而言，如果不能接受不能接受短期挫折，要求每一步都追求比上一步高要好，那么他也可能落入局部最高点。一点的眼前利益。

这就好比很多人在换工作时，都要求下一份工作的工资比当前的更高，但是殊不知，这种要求每一步都比上一步要好的方式，可能会让他落入局部最高点。。其实，如果是年轻人，应该更加用于探索，甚至接受下一步的如果新公司的行业前景更好，那他就应该接受当前的薪资比之前的要少，由此有机会进入一个眼前起点不高，但是潜力很大的退行业，从步，这样他在以后才能达到一个更高的高度。

破解办法：用随机的方式接受不完美

退火最终可以使所有的金属晶体达到完美的平衡状态，爬山算法中的随机性也是如此，随着时间增加慢慢降低。开始时我们要接受结果有较大的概率并不完美，而这个概率，会随着时间的增加慢慢降低。

我们还可以继续追问：我们以什么样的方式接受不完美。

其中一种方式是引入随机。我们可以略微修改一下爬山法：即使在当前的解xk周围随机找到的解 xk+1 不如 xk 大，我们也以一定的概率接受它。

从图16-3中可以得出，如果我们到了左边的这个局部最高点，那么这种方式可以使我们接受那个山脚下的点，跳出这个局部最高点并达到右边的全局最高点。

回到开头的那个问题：毕业之后，是回自己的家乡还是去大城市闯一闯？

人生其实是一个寻找最优解的过程。一开始谁都不是完美的，但是我们可以不断努力提升自己，最后的目标是达到自己可能到达的最优位置，这就是爬山法的基本思想：你需要争取每一步，都要比前一步更好。

但是，从上面的讨论中我们知道，为了避免陷入局部最优值，我们在不断进步的过程中，需要引入随机性：以一定的概率接受暂时的不完美，不必要求自己在人生中新迈出的每一步都比前一步更好。比如，换工作时，不必要求下一份工作的工资比现在更高或更稳定，这样才能有效避免陷入局部最高点，尝试各种职业，进而找到自己的兴趣、发现自己的潜力。

而模拟退火算法则进一步告诉我们，这个随机性应该随着你的年龄慢慢降低。所以，在年龄渐长、知道自己最适合什么后，你就要控制随机性，在自己最适合的地方深耕，不轻易切换赛道。

文章由科普中国-星空计划（创作培育）出品，转载请注明来源。

作者：北京航空航天大学副教授、博士生导师 刘雪峰

审核：华中师范大学数学与统计学学院 副教授 邓清泉