寻找现实世界中的“MOSS”（六）：不会犯错的量子计算机

在上一篇文章中，我们了解到了“拓扑不变性”这个有趣的特性，即外界环境的局部干扰无论多么剧烈，都无法改变系统整体的拓扑性质。因此，采用具有拓扑不变性的物理载体作为量子比特，就可以构造出具有容错特性的拓扑量子计算机，从而有望在未来实现真正通用的量子计算机。

量子计算概念图

（图片来源：Veer图库）

拓扑量子计算在理论上是一种近乎完美的方案，然而，要想在现实世界中寻找到具有这种神奇拓扑性质的物理载体，并不是一件容易的事情。

要想在偌大的世界中找到合适的载体，我们需要“睁大眼睛”，来重新认识我们熟悉的这个物质世界。

稳定不变的奥秘——马约拉纳费米子

一般而言，宇宙中的万物无论多么复杂，都是由两种基本粒子组成，即费米子和波色子。其中，费米子构成了各种物质，而物质之间的相互作用则由玻色子来传递。

原子示意图

（图片来源：Veer图库）

这就像一些游戏中的情景一样，物质世界是由一块块的砖块（费米子）堆叠组合形成的，玻色子则是砖块之间的黏合剂，二者相互作用，筑起世界之墙。

费米子就像组成世界的砖块，而玻色子则是砖块之间的黏合剂

（图片来源：Veer图库）

也就是说，构建物质世界的基本单元是费米子，而波色子负责告诉费米子如何传递相互作用，从而组成丰富多彩的物质世界。因此，我们要想在物质世界中寻找到合适的物理载体，从而具有拓扑不变性，就需要将搜索的范围缩小到“特殊的”费米子（具有拓扑不变性的费米子）上（而不是波色子），从而现可容错的拓扑量子计算。

早在1937年，意大利物理学家马约拉纳（Majorana）在进行理论计算时就意外地发现，存在一种特殊的费米子具有拓扑不变性。这种新奇的基本粒子因此被称为“马约拉纳费米子”。

意大利物理学家马约拉纳（Majorana）

（图片来源：Wikipedia）

自从“马约拉纳费米子”的概念被提出以来，无数的物理学家夜以继日地在实验中寻找它的蛛丝马迹。

直到2017年，华裔物理学家张首晟才首次发现了马约拉纳费米子存在的证据。遗憾的是，人们至今没有找到它。

因此，物理学家们不得不再次思考，如何才能找到与马约拉纳费米子具有相似拓扑不变性的物理载体呢？

终于找到你，马约拉纳零能模

为了实现拓扑量子计算，物理学家们可谓绞尽脑汁。尽管至今仍未发现马约拉纳费米子，但幸运的是，物理学家们终于找到了具有类似性质的“马约拉纳零能模 (Majorana zero mode)”。

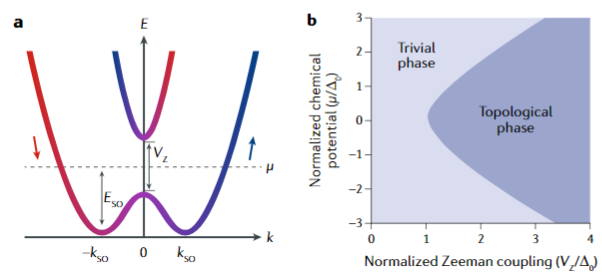
超导材料中的马约拉纳零能模 (Majorana zero mode)

（图片来源：参考文献[1]）

其实，“马约拉纳零能模”这一概念并不神秘，我们从名字就可以猜到，它是与马约拉纳费米子具有类似拓扑不变性的一种零能量的模式。也就是说，“马约拉纳零能模”是在某种特定的激发状态下存在的能量模式。

“马约拉纳零能模”之所以具有拓扑不变性，是因为这种能量模式下可以激发出等量的正反粒子。而正反粒子相遇后就会相互湮灭，从而形成中性的准粒子，从而具有与马约拉纳费米子类似的拓扑不变性。

在科学家们偶然发现“马约拉纳零能模”后，这种天才般的想法随后在实验中被成功验证。而这种具有拓扑不变性的“马约拉纳零能模”，也已经在超导材料的体系中被构造出来。

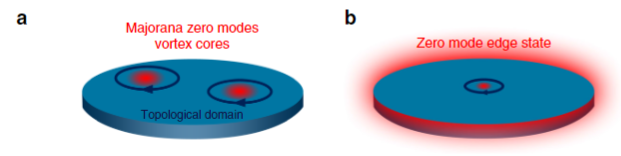
马约拉纳零能模的示意图

（图片来源：参考文献[2]）

马约拉纳零能模的出现，意味着量子物理学家可以借助超导材料中构造的“马约拉纳准粒子”，来实现具有拓扑不变性的量子计算机以进行真正容错的量子计算。

千呼万唤始出来，拓扑量子新进展

尽管马约拉纳零能模的出现为拓扑量子计算提供了更大可能，但物理学家们还需找到有效操纵量子比特的方法。为了达到这一目标，物理学家们可以通过交换两个不同的马约拉纳零能模，来改变量子比特的状态。这种交换马约拉纳零能模的方式，就像女孩子编织发辫一样，因此也被形象地称为“拓扑编织”。

2023年5月，来自谷歌的量子计算研究团队在《自然》期刊上发表了最新的研究成果。他们宣称，已经在超导体系的材料中构造并操纵了拓扑量子比特，并且实现了三个拓扑量子比特的演示实验。

谷歌量子团队在《自然》期刊上发表的拓扑量子新进展

（图片来源：参考文献[4]）

基于谷歌成熟的超导量子处理器架构，物理学家们将马约拉纳零能模进行了拓扑编织，并且进一步观察到了拓扑量子比特之间的纠缠现象。

这意味着，物理学家们已经可以初步地构造和操纵拓扑量子比特，以近乎完美的容错性和抗干扰性来避免量子计算过程中可能出现的运算错误。虽然现在只是小小的一步，但对于实现通用化的容错量子计算机而言，却是具有里程碑意义的一大步。

结语

拓扑量子计算，本身就是来自数学、物理学等多个领域科学家和无数工程师灵感的神奇碰撞。可以说，拓扑量子计算方案是人们对于量子时代的一次最大胆的想象。

拓扑量子计算的方案以其自身近乎完美的容错性和抗干扰性，吸引着无数科学家的持续关注。或许在不久的将来，我们将目睹通用量子计算机的诞生，它将以惊人的计算能力和革命性的应用改变我们的世界。现在，有越来越多的理由让我们相信，这一天即将到来。

参考文献：

[1] Lutchyn, Roman M., et al. (2018). Majorana zero modes in superconductor–semiconductor heterostructures. Nature Reviews Materials.

[2] Ménard, Gerbold C., et al. (2019). Isolated pairs of Majorana zero modes in a disordered superconducting lead monolayer. Nature communications.

[3] Tuovinen, Riku, et al. (2019). "Distinguishing Majorana zero modes from impurity states through time-resolved transport." New Journal of Physics.

[4] Google Quantum AI and Collaborators. (2023). Non-Abelian braiding of graph vertices in a superconducting processor. Nature.

作者：栾春阳（清华大学物理系）