植物也懂数学？神奇的斐波那契数列

编者按：植物在自然界中占有非常重要的地位，岁月流变、气候变迁、地质运动、生境更迭，植物历久弥新，在不断演化中保持着不息的生命力。中科院之声与中国科学院武汉植物园联合开设“芳草萋萋”，在这里，我们关注植物的生存、竞争、繁衍、死亡，展示自然界的奇特多姿，探索神奇的生命秘境，了解植物给人类带来的无限美好，致敬这无声无息又蓬勃多姿的植物世界。

▲植物中的数学美 图片来源：科学网

植物和数学，听起来似乎是两个风马牛不相及的研究领域，但是它们如何能扯上关系呢？这个问题，就需要科学来给我们解答了。科学研究工作者通过长期的观察分析惊奇地发现：自然界各种植物生长，在某些方面都合乎一定的数学规律。花瓣对称地排列在花托边缘，整个花朵几乎完美无缺地呈现出辐射对称形状，有些植物的种子是圆的，有些呈刺状，有些则是轻巧的伞状……所有这一切都向我们展示了许多美丽的数学模型。不仅如此，科学家们还发现某些植物的花瓣、萼片、果实的数目以及其他方面的特征，都非常吻合一个奇特的数列，世界上最著名的数列之一——斐波那契数列：1、2、3、5、8、13、21、34、55、89……

斐波那契数列的身世

13世纪意大利著名数学家斐波那契在他的著作《算盘书》的修订版中增加了一道兔子繁殖问题。问题大概是这样的：如果每对兔子（一雄一雌）每月能生殖一对小兔子（假设也是一雄一雌，下同），每对兔子第一个月没有生殖能力，但从第二个月以后便能每月生殖一对小兔子。假定这些兔子都没有死亡现象，那么从第一对刚出生的兔子开始，12个月以后会有多少对兔子呢？解释说明为：第一个月：只有一对兔子；第二个月：仍然只有一对兔子；第三个月：这对兔子生殖了一对小兔子，共有1+1=2对兔子。第四个月：最初的一对兔子又生殖了一对兔子，共有2+1=3对兔子。则由第一个月到第十二个月兔子的对数分别是：1，1，2，3，5，8，13，21，34，55，89，144， ……，后人为了纪念提出兔子繁殖问题的斐波纳契，将这个兔子数列称为斐波那契数列，即把 1，1，2，3，5，8，13，21，34…这样的数列称为斐波那契数列。这个数列有一个很明显的特征，第0项为0，第1项为第一个1，数列从第2项开始每个数字都是前二项之和。有趣的是，随着数列数值的增加，前一项与后一项之比越来越接近黄金分割的数值 0.618……因此，斐波那契数列也被称为黄金分割数列。

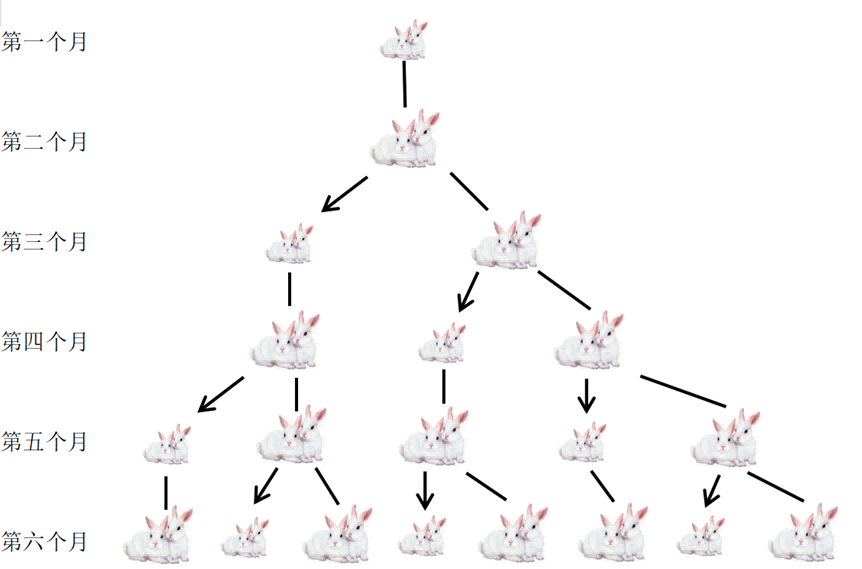
斐波那契数列中的任意一个数，都叫斐波那契数，在大自然中斐波那契数列的这些性质以各种各样的形式展现出来。大自然中的植物千姿百态，或许你没有留意，但实际上一些植物花、叶、果实中都包含着斐波那契数列。

种子与花朵的斐波那契数列

打开植物王国的大门，就会发现向日葵花盘内花朵的排列不是杂乱无章的，而是暗藏数学逻辑之美的哦！向日葵的花序中央的管状花和种子从中心点向外，每一圈数量分别为1、2、3、5、8、13、21、34、55、89、144、233......按照斐波纳契数列的规律排列，即后一数字为前面两个数字之和。还可以看到由中心点开始向外围延伸的螺旋线，在布满300朵管状小花的花序中就有34条左旋曲线和21条右旋曲线，其螺旋线的总数为斐波那契数。那向日葵为什么会这样排列呢，原来向日葵需要尽可能的繁育更多的后代，结出更多的果实，从而必须“考虑”空间上的经济性。向日葵花序尽可能安排多的小花管状花在一起，增强“小花群体”的吸引力，同时还需要减少小花之间的相互干扰，小花相互之间的重叠越少越好，保证这些小花拥有平均的空间，向日葵这样的数学排列的方式可以让种子在同等面积中容纳数量最多，花盘也变得最坚固壮实，产生后代的几率也最高。

▲向日葵花盘中的斐波那契数列 图片来源：researchgate.net

常见的菊科植物，诸如木茼蒿Argyranthemum frutescens和松果菊Echinacea purpurea的花盘都能看到斐波那契螺旋线，而且花盘越大越明显，向日葵只是一个典型代表。植物的花盘之所以呈现出斐波那契螺旋线，是因为这样的排列可以使种子得到最佳的堆集效果，彼此的生长空间相似，可以充分利用阳光和空气，有利于后代繁衍。松子在松果上的排列也遵循斐波那契螺旋线，当仔细观察松果时，可以观察到排列的螺旋图案，每个松果鳞片都会沿着自己的一组螺旋曲线向外延伸。

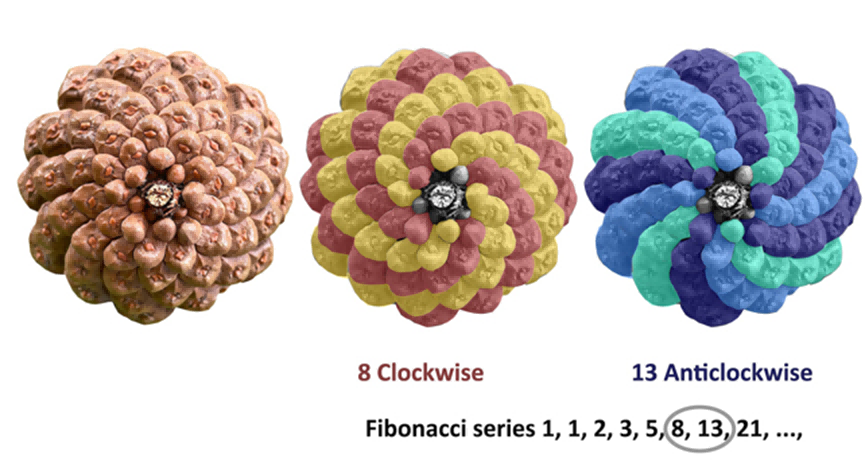
▲松果中的斐波那契数列 图片来源：fjjyxy.com& sciencealert.com

树木叶片的斐波那契数列

树木在生长过程中，由于新生出的枝条，往往需要“休息”一段时间，汲取储存更多的营养物质供自身生长，而后才能萌发出新的枝条。所以，一株树苗在一段间隔，例如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则次年“休息”。这样，一株树木各个年份的枝桠数，便构成斐波那契数列。换句话说，树枝的繁衍方式是按照斐波那契数列增长的。

按照这种排列模式，叶子可以尽可能多地获取阳光进行光合作用，或承接尽可能多的雨水灌溉根部。正因如此，建筑家仿照植物叶子在茎上的排列方式设计、建造了的新式仿生房屋，不仅外形新颖、别致、美观、大方，同时还有优良的通风、采光性能，凸显了黄金分割率的奇妙用处。

我们知道夏秋两季食用的像牛角一样的菱角，它来自于菱。菱的植株常见于池塘、河流和沼泽等水域，它的果实像牛角一样拥有硬实外壳但美味可口。仔细观察漂浮在水面上的叶片是否十分特别？叶片的排列方式呈螺旋状，每条螺线上的叶片数量，遵循着斐波那契数列，即1、2、3、5、8、13...... 不信你可以数数看。难道说菱懂得斐波那契数列吗?事实上并非如此，它们只是按照自然的规律才进化成这样。每片叶子从中轴附近生长出来，为了在生长的过程中一直都能最佳地利用空间(要考虑到叶子是一片一片逐渐地生长出来，而不是一下子同时出现的)，每片叶子和前一片叶子之间应该有合适的角度。螺旋状的排列方式保证了叶片互不遮挡且铺满水面，有利于菱的生长，是不是很有趣呢？

▲菱角果实 图片来源：quanjing.com

▲菱角叶片的斐波那契数列 图片来源：zhiwusuo.com

除此之外，叶片的分裂数与斐波那契数列之间也存在某种关系。例如：二裂坎棕、羊蹄甲叶片 2 裂，牵牛花、葡萄叶片 3 裂，五角枫、鸡爪槭叶片5裂，八角金盘叶片多为8裂等。

▲叶片裂数中的斐波那契数列 图片来源：中国植物志

花瓣的斐波那契数列

细细观察，我们就可以发现自然界中有1个花瓣的红掌花、牵牛花，2个花瓣的铁海棠、虎刺梅，3个花瓣的铁兰、三角梅。而最常见的花瓣数就是5，像桃花、梅花等都有5个花瓣，鸢尾花、百合花（看上去是6片，实际上是两套3片）是3片花瓣，还有8个花瓣的飞燕草、波斯菊，13个花瓣的瓜叶菊和万寿菊，21个花瓣的紫菀。向日葵的花瓣有的是21枚，有的是34枚，而大多数的雏菊都是34瓣、55瓣或89瓣，这些数字的花瓣在植物界很常见，而其他数字的就相对很少。这些数字如果排列起来，就是3，5，8，13，21，34，55.89……从中你发现了什么规律吗？那就是这些数字的前两个之和等于第三个，这也是斐波那契数列。

▲花瓣中的斐波那契数列 图片来源：csdn.net

其实，斐波那契数列与自然、生活、科学上的联系还有很多。斐波那契数列像一曲灵动而曼妙的音符，用它极其美丽又和谐的曲调谱写着大自然神奇美妙的节奏，而且斐波那契数列还把数学的对称美、奇异美、统一美等美的特性体现得淋漓尽致。生活中惊喜无处不在，植物中的斐波那契数列，就是大自然用它最独特的方式带给我们的科学启迪与艺术灵感，让我们感受到了大自然的和谐与数学世界的奇妙。

▲自然界中植物的斐波那契数列 图片来源：dashangu.com

来源：中国科学院武汉植物园

中科院科学传播研究中心

编辑 | 厉春

校对 | 李思瑾 曹瑞玥

审核 | 何勇