漂亮国的核潜艇与深度学习的内卷

漂亮国的核潜艇与深度学习的内卷

近日原本擅长长期潜水的漂亮国的核潜艇，频频抛头露面上热搜。先有拜登决定转让核潜艇技术给澳，釜底抽薪截胡高卢；接着又有顶级攻击核潜艇在中国南海撞不明物体，引来自媒体一阵狂欢，随后爆出的黄花鱼养殖箱被撞更具戏剧性想象空间。然而“核潜艇之王”如此先进的探测技术，怎么会“看”不到这些不明物体呢？

专业媒体给了答案，核潜艇讲究安静、深潜与高航速，首选预先准备好的详尽海图，而不使用主动高频声纳，目的是为了躲避反潜探测，因而无法及时感知到周围重要变化，比如一个移动的黄花鱼养殖箱。这有意无意间将核潜艇变成了巨大的活生生的有形的信息茧房。

哈佛大学法学教授、奥巴马的法律顾问凯斯·桑斯坦2001年在《网络共和国》一书中提出「信息茧房 Information Cocoons」，本来是一个抽象的概念，指人们接触的信息会习惯性地被自己的偏好所引导，从而将自己桎梏于像蚕茧一般的「茧房」中的现象。而这些巨大的核潜艇，却实实在在把自己桎梏在海图里，成了安静深潜的“茧房”，样子都颇为相似。

其实，现实中的无形的信息茧房无处不在，看头条，刷抖音，社交购物，都无法逃避算法构筑的一个个信息茧房，不知不觉中被种草杀熟割韭菜。不仅普罗大众如此，从古至今的“智慧”的先哲们，认知也不可避免的打上时代的烙印，偶有几个被外星文明量子纠缠过的，突破一层两层茧房的另类，或被当成异端，或成为人人敬仰的大神。

柏拉图手指天空：世界的本质是理念；亚里士多德手按大地：经验世界才是知识的来源；老子翩然一笑：道可道非常道。他们都是先哲，有足够的智慧突破自己时代的信息之茧。而世人多数没有这么幸运，即使诺贝尔大奖的获得者，都跳不出当时的主流思想框框，其中既有达尔文主义的经济学泰斗，又有虔诚于热力学熵理论的量子物理学家。

What is rational is real; and what is real is rational，这是黑格尔“存在即合理”的英文译文，与亚里士多德的说法一脉相承。“存在即合理”这句著名的中文译文却严重曲解了黑格尔的原意，形成了国内普通人对黑格尔认知的信息茧房。近一百多年来，知识的分支无论是在广度还是深度上的增长速度，已经使我们面临一个进退两难的境地，一方面人类的知识应该融汇贯通成一个整体，另一方面，领域的不断专业化，让彻底掌握它们变得几乎不可能。然而“对于统一的、普遍性的知识的不懈追求，是我们从先辈那里继承下来的最好品质“，薛定谔说。

人类的科学理论，从地心说到日心说到现在的“宇宙心说”，其实都是对人类所处的大宏观物理系统的盲人摸象，而且只缘身在此“茧”中。设想混沌无序的最大熵系统被黑洞吞噬，能量质量又一次的轮回，我们观测的熵增熵减规律或许仅是宇宙的一次潮汐。然而亚里士多德影响了西方整个科学实践，通过总结“经验世界”获取科学“知识”，这也是机器学习与深度学习的深层的哲学基础。

所以，我们的机器学习深度学习科学家们，发明了众多的先进的学习算法，基于大数据或者大样本，用这些算法去探索和挖掘“经验世界”中蕴含的规律或”知识“。玻尔兹曼机 Boltzmann Machine，变分推断 Variational Inference，重整化群 Renormalization Group，生成对抗网络 Generative Adversarial Network，逆向强化学习 Inverse Reinforcement Learning，这些如日中天的名字都曾经激发了人们对通用人工智能的遐想 -- AI 有了自己的思维，人类迭代出了新物种。

“我思故我在”又一个严重曲解的中文译文，这里不深究。可“思”究竟是什么呢？笛卡尔解释道，“一个在怀疑，在领会，在肯定，在否定，在愿意，在不愿意，也在想象，在感觉的东西”。籍此，笛卡尔建立了其思想的绝对坐标系。而我们的这些推陈出新的算法究竟在做些什么呢，它们在“思”么？

《站在香农与玻尔兹曼肩上，看深度学习的术与道》中我提到，深度学习领域的三类最典型问题，无监督学习Unsupervided learning，有监督学习的分类Classification与预测Prediction，归根结底都是用神经网络来近似概率分布：想象一个（x,y）的联合概率分布，或y发生条件下，x的条件概率分布，或互换，训练的过程就是找到这个近似概率分布函数的过程。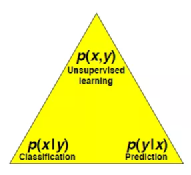

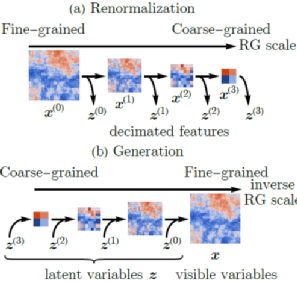
《薛定谔的滚与深度学习中的物理》文中我进一步做了梳理：玻尔兹曼机 Boltzmann Machine 践行了重整化群 Renormalization Group 的思想，事实上，在神经网络中引入隐含节点就是尺度重整化。每一次尺度变换后，自由能保持不变。F =-lnZ, 这里Z是配分函数，是一个能量（不同能级上粒子数）的概率分布，Z不变，即能量的概率分布不变。重整化群给出了损失函数，也就是不同层的F自由能的差异，或者说两个能量概率分布的“距离”， 训练就是来最小化这个距离。

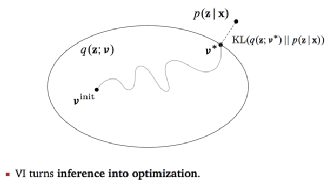
变分推断 Variational Inference来的更直接，其目标就是根据已经掌握的数据或样本，推断需要的分布 p(z|x), 当p(z|x) 无法直接求解时，先根据经验找到一个可能的近似分布 q(z; v), 然后逐步缩小 p(z|x) 与 q(z;v)的差异，也就是缩小这两个分布的某种意义上的“距离”，例如下图中常见的KL散度距离。当这个距离足够小的时候，q(z;v*) 就成了 p(z|x)的近似分布。核心思想是将求解概率分布问题，转换成了距离最小化的优化问题。

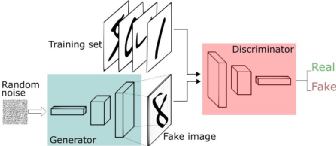
对于生成对抗网络 Generative Adversarial Network，Ian Goodfellow（GAN之父） 给过直观的比喻：“印假钞的罪犯不断伪造更逼真的钞票（生成器），警察则竭力判别真钞假钞（判别器）”，在道高一尺魔高一丈的对抗中，双方都得到提升。魔道双方努力的方向本质上是同一件事：真实样本（真钞）和生成样本（假钞）之间的差异，魔不断努力缩小这个差异，道训练火眼金睛判断这个差异。数学上样本差异通常用其概率分布的距离来度量，比如大家熟悉的交叉熵（cross entropy）：H(p,q) := -E [p(x) logq(x)]

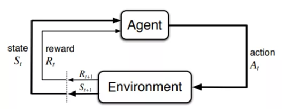
《薛定谔的小板凳与深度学习的后浪》中我又探讨过强化学习：通过让软件定义的智能体（Agent）与环境（Environment）交互来训练模型。当智能体的行为（Action）产生期望的结果时，智能体将获得激励（Reward），也就是环境给它这个行为正面或者负面的反馈，促其成长到新的状态（State），这一行为也将被强化，塑造智能体在此环境下，后续的良好行为。这一交互过程持续迭代，智能体在奖励或惩罚中不断的“学习知识”，“积累经验”，从而更加适应环境。

如文中所述，复杂场景特别是多智能体的博弈下，给出激励（Reward）是极其困难的，多数情况几乎不可行。逆向强化学习 Inverse Reinforcement Learning 则帮我们找到了一种高效可靠的激励方法：通过收集专家的经验与环境信息，来反向学习激励函数。

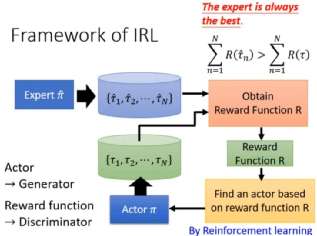
聪明的读者可能已经注意到，如此改造后的强化学习，其实像极了生成对抗网络：只不过GAN中的左右手互博的猫和老鼠的对抗，变成了这里的专家对智能体的循循善诱的“激励与辅导”。学习效果的好与坏的标准，本质上是比较专家样本分布，与智能体行为样本分布的差异，最小化这两个分布之间的距离。

玻尔兹曼机 Boltzmann Machine，变分推断 Variational Inference，重整化群 Renormalization Group，生成对抗网络 Generative Adversarial Network，逆向强化学习 Inverse Reinforcement Learning，其实都是在做一件事：通过学习，不断缩小模型学到的概率分布与样本概率分布之间的距离。枯燥的算法到此，突然变得非常有趣。尽管大家的出发点不同，目的地却都是一样的。然而还有一个小问题没有解决，大家对“距离”的判断不尽相同:

欧氏距离，曼哈顿距离，切比雪夫距离，闵可夫斯基距离，马氏距离，余弦相似度，皮尔逊相关系数，汉明距离，杰卡德相似系数，编辑距离，KL 散度，还有改进KL散度的对称的JS 散度。看到了吗，世界原本十分简单，却被人们弄得如此复杂。

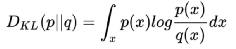
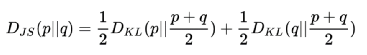
那是否可能存在一统天下度量衡的某种“距离”？答案是肯定的。但故事得从18世纪末路易十六统治下的法国讲起，蒙日是当时最杰出的科学家，他在研究如何以最小的成本把农场生产的牛奶分配给工厂的奶酪工匠们的高深问题。如果你做过供应链规划，你会感同身受。这个看似简单的问题就是著名的蒙日问题，数学家们用了近200年才完全刻画这个问题。苏联数学和经济学家Kantorovich因对此问题的研究和最优资源匹配的贡献获得了诺贝尔经济学奖。

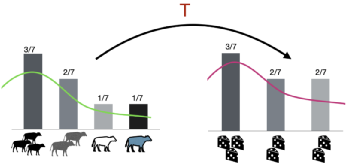
简单理解，这个问题可以抽象成：供应分布 X [x1, x2, x3, x4, …, xn ] 到需求分布 Y [y1, y2, y3, y4, …, ym ] 的最小成本的运输问题 ( cost_ij = xi -> yj )，也就是著名的最优运输（Optimal Transport）问题。从连续的视角看，该问题就是将供应概率分布p(x) 转变成为需求概率分布q(y)。设转移成本（距离函数）为d(x,y)，我们得到一个距离定义：

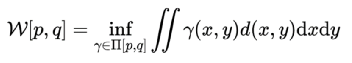
这两个概率分布之间差异的度量就是 Wasserstein距离。它规避了KL散度和JS散度的许多痛点问题。从目前它在各个领域的算法研究中的热度来看，大有一统天下的趋势。如果距离统一这一天到来，玻尔兹曼机，变分推断，重整化群，生成对抗网络，逆向强化学习，在Wasserstein距离意义上也将实现殊途同归。从另一个侧面，我把这也看作深度学习领域的Wasserstein距离意义上的内卷。好比儿童发热，去多家医院各种检查，最后的药方可能都是美林。

解决同一个问题，以农民心态工匠精神，精益求精多探索几个方法是无可厚非的。问题最终可能出在最大似然估计 Maximum Likelihood Estimation上，或者是加了先验正则项的最大后验估计Maximum A Posteriori Estimation上。

在《薛定谔的佛与深度学习中的因果》中我总结过，最大似然就是找到一组权重 w*，使得观测到的数据集 D 出现的可能性最大：Max (p(D|w*)) 。而学习这个权重w，就是不断看到训练数据后，持续改变我们原来对权重参数的认知。注意这里的逻辑，“观测到的数据集 D”事实上决定了你的模型可以学习到的极限，它成了所有学习方法的信息茧房。也就是说，所有的努力学习都不得不在此茧房之内互相“卷”。

所以，当Wasserstein距离完成统一大业，最优运输将主导机器学习领域，模型之间的差异将很大程度上取决于观测到的数据集，也就是观测样本在时间空间维度上的广泛代表性。未来机器学习领域的竞争，将演化为样本采集方式方法和代表性判断等领域的竞争。这可能是为什么Andrew Ng更推崇“数据量驱动机器学习过程”，还举办了以数据为中心的 AI 竞赛，侧重奖励“数据提升Data Boosting”技术方向的创新。

不过适度卷卷有时候是好事。今年诺贝尔物理学奖颁给了复杂系统研究领域，这是又一次概率的思想与方法的胜利。从更大尺度看问题，让小尺度的随机系统具备了统计意义，也就使得发现确定性的统计规律成为可能。CNN提取的图像的FeatureMap, RNN Attention的自然语言的Context Vector, 傅里叶/小波变换出来语音的频谱，其实都是隐含尺度上的确定性规律，而深度学习可以帮助发现这些规律。

大学University在英文中与普遍性同义，自从其产生以来，历经数个世纪，无不暗示着普遍性才是我们追求的永恒价值。最大似然下的机器学习隐含着平均稳定的普遍性思想，可以帮助人们找到复杂事物中的趋势与周期。然而高维度确定性的混乱充斥人们的日常，这也是世界如此丰富多彩的源泉。一方面我们期待稳定的趋势与周期判断，一方面借助高维度确定性的混乱，冲破束缚我们认知的信息茧房。

参考资料：

https://arxiv.org/pdf/1608.08225.pdf

https://arxiv.org/abs/1701.07875

https://ai.stanford.edu/~ang/papers/icml00-irl.pdf

https://arxiv.org/abs/1601.00670

https://arxiv.org/pdf/2102.02454.pdf

http://rail.eecs.berkeley.edu/deeprlcourse-fa18/static/slides/lec-16.pdf

https://towardsdatascience.com/optimal-transport-a-hidden-gem-that-empowers-todays-machine-learning-2609bbf67e59

作者：王庆法，数据领域专家，首席数据官联盟专家组成员