GPT4技术原理三：重整化群与生成式AI

GPT4技术原理三：重整化群与生成式AI

虽然微软科学家Bubeck宣称传统机器学习已经不存在了，但是 AI 物理学还是实打实继续存在的，而且还有可能在大模型时代爆发。本文是GPT4技术原理探索系列第三篇，探讨一下重整化群与大模型的训练和生成的背后机理。

“熟读唐诗三百首，不会作诗也会诌”- 鲁迅

鲁迅先生可能很谦虚说这话不是他说的，但是却不经意间道出了大模型成功的真实逻辑。在熟读天下文章三百T之后，大模型开始会诌“人话”了，而且头头是道。保守派学者认为大模型不过是“一本正经的胡说八道”，但仔细想想谁又不是”一本正经的胡说八道”呢？李白的诗句最典型：“白发三千丈，缘愁似个长”，“危楼高百尺，手可摘星辰”，“桃花潭水深千尺，不及汪伦送我情”，“飞流直下三千尺，疑是银河落九天”，哪句不是一本正经的胡说八道？而且保守派学者没有深入研究 AI 物理学，就妄下结论，本身不也是某种意义上的“一本正经的胡说八道”？！

言归正传，GPT4技术原理二：相变与涌现中我们提到，重整化群（下文简称RG: Renormalization Group) 是研究不同尺度下对称性破缺与重建过程的核心数学手段。借助RG，人们可以在不同尺度上分析、观察系统的特性。这是分层次结构化的认知思想，人们每天都在实践。

为更好的理解RG，我们需要回顾一下”群（Group）“这一看似高深的数学概念。笔者大二还在学习数学分析、线性代数的时候，误选了数学系研究生课程《李群与外微分》，还退不了，只好硬着头皮一头雾水的听完。全程窘迫但是一个巨大的收益是，从此笔者不再对各种花样玄妙的数学概念心生畏惧，即使仍然敬佩。实话实说，很多玄妙的概念是因为翻译导致的，比如这里的”群（Group）“，比如”重整化“。

重整化群，李群，微信群，QQ群，这里”群“其实本质都是一个意思，英文是Group。就是一“组”什么事物，因为某种意义需要放在一起。群有群约定的规范，有了规范才具备这里的”某种意义“。这些约定的规范决定了群与群的不同，也就是这些约定的规范定义了群。记得当年笔者为了理解什么是群，翻遍了图书馆能见到的中文著作，一个比一个复杂抽象，满篇的公式，没有见到特别直观intuitive的阐释。

那数学上的群到底是什么意思呢？其实本质很简单。数学上的群，就是定义了一组变换（Transformation），或者也可以叫操作（Operation）。群成员是一组Operator 或者 Transformer，你联想到了大模型的Transformer? 酷，不过这里还是泛指变换，我们下文再谈跟LLM Transformer的关系。如果我们用G 表示群，则G(X)就表示将群定义的变换或操作作用在对象X上。有别于微信群的群，数学上定义了这一组Operator （ 这里我们用E,A,B表示这些Operator ） 之间应该满足的关系：

任何两个operator相乘（AB）的结果还是群中的operator。相乘就是一个operator作用完，另一个operator再作用在其结果上, AB 就是B先作用，然后A作用;

存在单位operator E, 就是此operator作用在对象上，对象不变，E(X) = X；

如果AB=BA=E, 我们称AB互逆, 每个operator 都得存在逆；

(AB)C = A(BC) 满足可以互相结合，先算括弧里的，这个估计大家都熟；

你可能还是觉得operator听起来玄乎抽象的，笔者为写好此篇介绍，又去清华图书馆数学专著中寻觅，找到一本英文的最直观的讲群的书，剑桥大学出版社去年出版，作者是MIT学者。《An Introduction to Groups and their Matrices for Science Students》，笔者觉得本书作者Robert Kolenkow 是能够化繁为简，深入浅出娓娓道来的大师。大家可以支持他一下。本文不是小红书种草文，是发自内心的佩服，笔者真期望大二时候看到这本书。

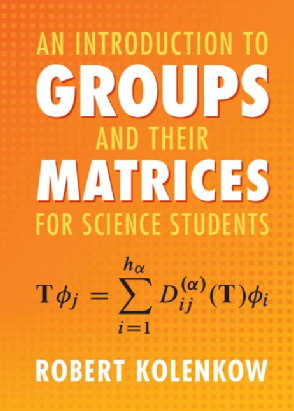
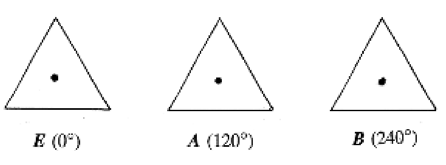
引用一个书中的经典例子，正三角形的旋转，E 是转0°，A是转120°，B是转240°。大家看看这三个Operator组成的群是不是满足上述的约束？好的，这个就是经典的Abelian Group。

大家可以自行阅读此书哈，书中详述了这些变换存在对应的数学上的矩阵表述。笔者在”迷人的数据与香农的视角“一文中整理过：” 任何一个mxn的矩阵A, 都可以分解成三个矩阵的乘积， UEV’, U,V都是正交基组成的方阵，E是对角阵（可以不是方阵）“，”想象空间中的一个点（也可以叫向量）到另一个点的运动，也就是从一个向量变成另一个向量。其间发生了什么？从几何意义上看，不过是一个向量分解到V上，然后分别做E描述的拉伸，再分解到U上。这个点到点的运动系统对外展现的信息用A表达了出来，而A中蕴含的动作是，在某些特定方向上的拉伸，也就是这个UEV中包含了A的潜变量，描述了运动的尺度与角度，在赋范空间，还会有长度，距离，体积这样的概念。“

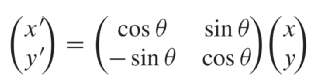
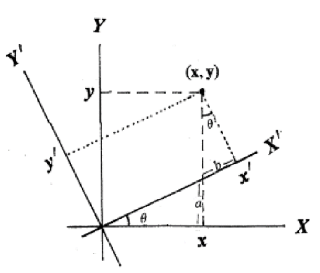
矩阵对应着某种变换，群中定义的这些变换可以转化为相应的矩阵形式。这里注意我们提到这个变换是从一个固定坐标系角度观察事物(x,y) 旋转拉伸变成了（x',y'），而从另一个角度看来，（x, y)其实也可以认为没变，变得是观察者的新坐标系（X,Y) 变为（X',Y'）。这个不起眼的”脑筋急转弯“带来了我们观察世界翻天覆地的认知变化。也就是，事物（比如一幅图像，一篇文字，一段语音）可能在其原始的坐标系（坐标系的维度通常可以类比事物的自由度）表现为极其复杂的形态，而在另一个坐标系（比如低维度或者说低自由度）下面表现为及其简单的形态。复杂是终极的简单。

笔者在”薛定谔的佛与深度学习中的因果“中提到，“事物由不同层次的随机变量展现出来的信息来表达，不同层次上的随机变量携带不同的信息，共同组合影响上一层的随机变量的信息表达，而随机变量对外表达的信息则取决于该随机变量的条件概率分布”。底层的多个独立的随机变量，如果都服从高斯分布，根据上文描述的特性，可以推断，一层层堆叠构成上层的随机变量之后，仍然服从高斯分布。而这个多个独立的服从高斯分布的随机变量的堆叠过程，就是典型的高斯过程。高斯过程是高斯概率分布在随机函数空间的表现形式。

聪明的你可能很快注意到，这里说的不同层次的随机变量有很好的性质，就是服从“高斯分布”。比如人们认识一张人脸，从眼角、眉梢、到额头、五官，脸型，神态都可以捕获不同层面的信息。浓眉大眼是你，神采奕奕也是你，都是从脸上蕴含的信息读取出来的。这些“眼角、眉梢、到额头、五官，脸型，神态”都可以是随机变量，但他们大都是围绕平均样态的些许偏离，都是符合大数定律的偏离。而大数定律体现出这些变量的高斯分布规律。这些高斯分布的不同层次的随机变量叠加就构成了这张脸。认知这张脸的学习过程，是逐层提取这些潜在随机变量的过程，而生成人脸图像的过程就是逐层采样恢复并堆叠这些随机变量的过程。

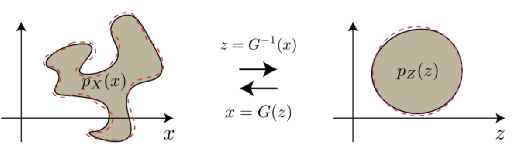
这里，如果用Z代表这张脸，借助我们刚才学会的群的数学形式可以表达为：G(Z) = G1G2G3G…Gn( Z )。这里的G1到Gn对应不同层次上Operation 或者说Transformation，也就是在各个层次的潜变量（“眼角、眉梢、到额头、五官，脸型，神态”）构成的新坐标系里面的矩阵代表的变换。大家知道，这些潜变量都是对应着简单的高斯分布的，其实都是个随机函数，Gx(Z)也就是Z这张脸在这些潜变量函数基张成的空间中的样子。概率分布是归一的，也就是normalize, 反复的normalize就是renormalize. 大家看看，“重整化”翻译的多么误导。但约定俗成，我们只能用这个。这其实就是重整化群学习和生成图像的本质。简单是终极的复杂。

在”漂亮国的核潜艇与深度学习的内卷“（此文是笔者多年感悟的重要总结，请一定认真多读几遍）一文中，笔者总结过：玻尔兹曼机 Boltzmann Machine 践行了重整化群 Renormalization Group 的思想，事实上，在神经网络中引入隐含节点就是尺度重整化。每一次尺度变换后，自由能保持不变。F =-lnZ, 这里Z是配分函数，是一个能量（不同能级上粒子数）的概率分布，Z不变，即能量的概率分布不变。重整化群给出了损失函数，也就是不同层的F自由能的差异，或者说两个能量概率分布的“距离”， 训练就是来最小化这个距离。

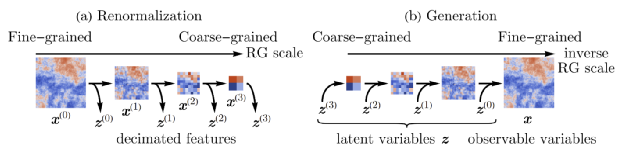
我们中科院的学者对这一领域有重要的贡献。上图是RGFlow论文（https://arxiv.org/abs/2010.00029）中的最重要的一张图。对一张图像，重整化从细颗粒度到粗颗粒度，逐层提取潜变量Zn, 提取图像中蕴含的各层次的结构；而生成图像的过程就是从粗粒度，对潜变量的高斯概率分布进行采样，重建下一个层次的结构（类似你跟别人描述这个人浓眉大眼）。重整化的群变换Gn 在生成过程中用到 Gn的逆。GPT 和其他大语言模型的使用的Transformer其实就可以类比这些重整化的群变换G，但是目前没有看到学术研究Transformer 是否严格有逆，也就是是否构成严格意义上的群。

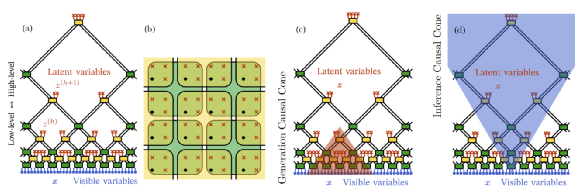
这是RGFlow 训练与生成模型的刨面图，当这个RG 模型看到过海量的人脸之后，它提取了来自广泛样本的人脸的各个层次的结构信息。生成的时候从中采样即可，记住，这些结构信息都是体现为联合概率分布，这些采样都是在高斯的堆叠的联合概率分布中采样，然后通过RG 的operation 的逆运算，算出你想要的图像。仔细体会一下，如果这个技术应用于文本，也就是熟读文章300T, 出口成章也就不足为奇了。有些自媒体剪刀浆糊讲的预测下一个单词，其实就是采样生成技术。鲁迅先生说的是对的。

然而，机械的熟读文章300T ，没有涌现也是做不到如李白一样文思泉涌的。上篇笔者提到：RG提供了一种研究微观细节如何产生较大尺度新涌现特性的方法。其实当初科学家将RG用于研究连续相变临界现象时，发现系统在不同尺度上，临界点附近表现出的自相似，能用RG很好的描述。RG成为连续相变合理有效的理论表述，而连续相变则成为RG的物理基础，重整化群的不稳定不动点对应了相变的发生。

根据“系列文章深度解析ChatGPT获得智能的数学物理机理“ 中的计划，下篇我们看看Transformer与能量模型，RG可以作为其有效的建模方法。

作者：王庆法 麻省理工学院物理系学者，数据领域专家，首席数据官联盟专家组成员