基于气动能量平衡点的微小卫星纯磁控方法

摘 要：针对气动压心不在质心后的低轨道小卫星主动纯磁控三轴稳定，提出了一种结合气动能量平衡点分析和周期系统稳定性理论的控制方法。首先将气动力矩写入姿态运动模型，建立卫星气动姿态运动方程，然后采用Lyapunov能量法建立卫星能量函数，求解卫星在无控状态下的气动能量平衡点。接着建立平衡点处的包含气动力矩的磁控模型，采用一种基于Gill因子的状态转移矩阵求解方法，然后根据周期系统稳定性判断方法进行控制参数选取。最后针对卫星的两个气动能量平衡点分别进行控制率的设计与仿真验证，仿真验证的结果是卫星精确稳定在对应的平衡点上。

Study on attitude control of micro-satellitewith only magnetic actuators based on air-energy balance pot

Abstract：For micro-satellite in the low orbit, the aerodynamic torque becomemore and more non-negligible. To study the balance position of themicro-satellite under periodic attitude control using only magnetic actuatorswhile bearing the unbalanced aerodynamic torque, we firstly establish energyfunction based on the air-attitude-motion equation which reflects the energy ofthe satellite and then solve the air-energy-balance pot. Then we establish themagnetic periodic control model at the balance pot, then we put forward a wayto solve system monodromy matrix based on Gill factor for stability criterion. Finally,we choose the control parameter for the periodic model on the twoair-energy-balance pot and do the simulation, the system has an excellentperformance .

Keywords：Micro-satellite Air-attitude-motion equation Air-energy-balance pot Monodromy matirx

0 引 言

微小卫星具有重量轻、体积小、功能密度高等优点，在过去的几十年中已经称为航天领域研究的一大热点，而在低轨道小卫星技术研究中，姿态控制系统更是作为关键的研究内容之一。在姿态控制系统研究中，磁力矩器由于其成本低，不消耗工质，等优点在低轨道小卫星姿态控制系统得到广泛应用，以磁力矩为单一控制部件的主动磁控方案逐渐成为研究的热点。

Micro-satellite has the advantage of light weight, small volume andhigh functional density,and has becoming the hot pot in the field of aerospacefor decades. In the research of low-orbit satellite technology,

对于纯磁控方案的研究大多停留在理论的层面，虽然很多学者对于纯磁控进行了多种控制率的设计，例如文献[1]采用的是能量磁控的方法进行了控制率设计，而文献[3]~[8]分别采用了周期连续系统和周期离散系统的理论进行纯磁控控制率的设计，而文献[9]~[13]采用了LQR、鲁棒、LTV、MPC和滑模变结构等现代控制理论的方法进行控制率设计。在以上从理论层面进行控制率设计的过程中，未考虑到工程实际中低轨道小卫星气动力矩对稳定位置的影响，或者仅仅是设定气动力矩为星体姿态运动的稳定力矩而不考虑气动力矩是影响星体姿态运动的干扰力矩时对于姿态稳定位置的干扰[1]。在工程实际中，气动压心不一定在质心的后方，即气动力矩不一定能为卫星姿态控制提供恢复力矩，文献[14]说明了质心与形心的相对位置对低轨立方星姿态控制精度影响很大，但是未给出在气动力矩作用下系统的平衡位置，且并未把气动力矩考虑到模型中去。

目前已经成熟应用于卫星上的有主动磁控与重力梯度稳定或者偏置动量结合的方案，例如丹麦的Orsted卫星是采用主动磁控与重力梯度稳定结合的方案[15]-[17]，美国海军的NPSATl卫星采用的是主动磁控与偏置动量结合的方案[18]，以及丹麦Alborg大学的AAusat系列卫星采用的放宽稳定条件仅实现某一轴对地定向的控制方案[19]，对于纯磁控三轴稳定方案尚不存在较好的应用的例子。

本文首先在文献[1]提出的能量磁控控制率的基础上，建立卫星气动姿态运动方程，建立了包含气动力矩的卫星的能量函数，求解了无控状态下两个气动能量平衡点。然后在平衡点处建立包含气动力矩的磁控周期系统的模型，采用一种基于Gill因子的状态转移矩阵求解方法，最后根据周期系统稳定性判断方法进行控制率设计[4][20]。

1. Lyapunov****能量法求解考虑气动力矩时姿态平衡点

1.1****卫星气动姿态运动方程

卫星的姿态动力学方程为

低轨道小卫星的干扰力矩主要是重力梯度力矩和气动力矩，表达式分别如下所示

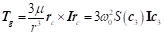
对于低轨道上运行的小卫星，单独采用磁力矩器进行主动控制时，气动力矩已经不能单纯的作为干扰力矩进行分析。在本文的分析中，将重力梯度力矩力矩和气动力矩作为系统模型的一部分，对应的姿态动力学和运动学方程如下

1.2考虑气动力矩时卫星能量函数及平衡点解算

卫星的总能量可以分为动能和势能，其中动能主要是由卫星角速度引起的，势能主要是由重力梯度力矩、气动力矩和卫星的陀螺效应引起的，卫星能量的求法如下

其中各个能量的表达式为

在求出卫星的能量函数后，能量函数的极小值点即为卫星的气动能量平衡点。

**2.**纯磁控三轴稳定控制率设计

2.1****平衡点处磁控模型的建立

根据包含气动力矩的卫星的运动学和动力学模型，可得非线性状态方程如下