洛希极限

名词概观

潮汐力

任何一个有质量的天体总是会对其它天体施加万有引力，而引力随两天体之间的距离增加而减小，因此站在受力天体的角度，位于其表面的单位质量与位于质心处的单位质量所受的引力会由于到引力源的距离不同而存在微小差别，我们将这个引力差称为潮汐力。对于受力天体来说，潮汐力会沿该天体质心与施力天体连线方向拉伸该天体，且两天体相距越近，潮汐力就越大，该天体就越容易被拉扯碎裂。1

物理图像

潮汐力会随着两个天体的距离减小而增加，所以在两个天体逐渐靠近的过程中，如果它们的密度足够大，而且为两个天体相互接近留下了足够的空间，那么就会存在一个极限距离，在该距离之内，其中一个较小天体恰好因为潮汐力而开始瓦解。在最初计算这个极限距离时，为了使模型更加简洁，不妨假设即将碎裂的天体仅依靠引力结合在一起（事实上像地球这种固态行星作为一个整体，它的组成物质相互之间还会有应力将彼此连接在一起），此外我们还假设在解体前，该天体形状保持一个完美的球形，那么显然，当该天体表面物质受自身的引力小于潮汐力时，其表面物质就会脱离，因此，洛希极限就是计算潮汐力等于自身引力时的距离，我们把以该种方法计算的极限距离称为洛希极限。但实际中，天体不一定仅由引力结合在一起，也不可能是一个完美的球体，所以天体解体的距离并不严格等于使用刚才方法所计算的洛希极限，因此需要对模型进行修正。

计算方法

潮汐力

因为洛希极限定义为受力天体恰好开始瓦解的距离，也就是只需要根据受力天体所受潮汐力竖直分量最大的一点处是否开始瓦解即可判断洛希极限的位置，所以此处就不给出潮汐力完整的证明，只计算潮汐力最大一点处的潮汐力。而这个潮汐力竖直分量最大的点就位于受力天体距施力天体的最近处。2

设施力天体质量为M、施力天体与受力天体质心距离为d、受力天体半径为r。

根据牛顿万有引力定律，受力天体质心加速度大小为。而距施力天体最近处的加速度大小为，则根据定义，潮汐力对应的加速度为。使用泰勒展开，可将展开为，在讨论中可以认为r<<d，因此将的高阶项近似为零，可得潮汐力为。

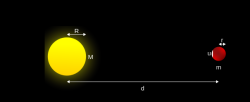
计算洛希极限

假设受力天体仅依靠自身引力维持形态、受力天体的形状是完美的球形，且在到达洛希极限前不因潮汐力而变形。

考虑受力天体表面最接近施力天体处的部分质量为μ，有两股力作用在μ上：受力天体自身对它的引力和施力天体对它产生的潮汐力。

设F**G为受力天体作用在μ上的引力，根据牛顿引力定律，。

设d.为受力天体与施力天体中心的距离，r为受力天体半径，F**T为施力天体作用在μ上的潮汐力，

若受力天体刚好位于洛希极限处，则有FG=F**T，即

由此即可计算出

一般我们不希望受力天体的半径出现在公式中，因为洛希极限实际上是由天体密度等更基础的性质决定的，因此将公式中的半径以密度等量写出。

施力天体的质量可写成：

受力天体的质量可写成：

代入上面的洛希极限的公式，得

简化成：

公式修正

刚体洛希极限

上文所计算的洛希极限实质上就是刚体洛希极限，它是默认受力天体不会形变且仅由引力结合这两个近似下的物理模型。这种模型很适合讨论例如碎石堆小天体、彗星等天体，对于类似于地球这样的天体可以近似讨论，但由于地球组成物质之间彼此绑定的应力，单纯刚体洛希极限的计算结果会与地球这种相对彗星大很多的行星的实际情况有所差异。

流体洛希极限

流体洛希极限与刚体洛希极限相对，在这个模型下我们假设受力天体是完美的流体，因此即使天体间距超过洛希极限，潮汐力会将受力天体拉长，从而导致潮汐力增加，进而导致其更容易碎裂。洛希所给出的公式为：

更精确的公式为：

可见它的系数比刚体洛希极限的大。

现实中，大部分天体都介于完美刚体与完美流体之间，因此它们真实的洛希极限介于刚体与流体洛希极限之间。

其它结合力

现实中，使天体紧密结合的力并不只有引力。以地球为例，地球大气除了靠引力维系，大气之间还存在粘滞力、摩擦力，这些力都会使地球更难以被撕裂。因此到达洛希极限时受力天体不一定会被瓦解。

所以在讨论一些如人造卫星等物体时，通过使引力等于潮汐力计算出来的洛希极限完全不适用了，卫星内部的结合作用远远大于引力。

应用举例

轨道半径与洛希极限比值

下表展示了太阳系内天体所处的轨道与洛希极限之比，可以看出很多卫星处于刚体洛希极限与流体洛希极限之间，而很少有天体位于刚体洛希极限之内。3

|| ||

苏梅克-列维九号彗星

苏梅克-列维九号彗星是一颗太阳系内的彗星，它在1994年7月17日4时15分与木星撞击，为科学家对木星的研究提供了很大的帮助。4

有趣的是，这颗彗星并未直接撞击木星，而是在距离木星表面约四万公里时分解成了21个碎块，这正是因为彗星达到了它在木星周围的刚体洛希极限。