伯努利原理

表达式

即伯努利方程。其中，为流体中某点的压强，为流体在该点的流速，为流体密度，为重力加速度，为该点所在高度，是一个常量。它也可以被表述为：

适用条件

伯努利原理并非适用于全部流体，而是只适用于描述理想流体的运动。因此要求流体满足：

1. 具有连续性：理想流体在任何给定的流动状态下都能保持连续性，即在任何给定的时刻和位置，流体的质量和体积都是连续分布的。
2. 不可压缩性：理想流体在流动过程中保持体积不变，即体积几乎没有变化。
3. 无黏性：理想流体没有黏性或称为无黏性，即在理想流体中，分子之间没有内部摩擦力，流体在外力作用下可以自由地流动。
4. 流体沿流线运动，流线彼此不相交。2

推导

伯努利方程可以分别由牛顿第二定律以及能量守恒定律推导得来。

牛顿第二定律推导

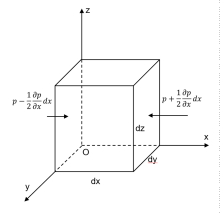
如图，取液体中的一微体，对于x方向，作用在微体上的力有两个方向的压力、以及体积力，X为体积力项系数，由牛顿第二定律可得

其中，为微体在x方向上的速度。化简可得

同理可得

同样，分别为微体在y方向和z方向上的速度。

将上面三式相加化简可得

对于理想流体，为常数，在重力场中X=Y=0，Z=-g，于是可将上式化简，得

即

1

能量守恒定律推导

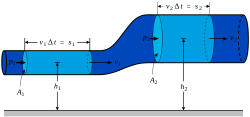
如图所示，假设理想流体在一个管道中中流动。设 W 表示在面积 A 上施加压力 p 所做的功，为引发的体积变化量，在1、2两个点的压力做功分别为

两点压力做功之差为

同时，由能量守恒定律可知，压力做功之差应等于动能和势能差之和

由上述两式可得

整理，得

将密度代入，得

图文解释：

丹尼尔·伯努利在1726年首先提出时的内容就是：在水流或气流里，如果速度小，压强就大，如果速度大，压强就小。这个原理当然有一定的限制，但是在这里我们不谈它。别莱利曼的书4里有几个通俗易懂的例子：

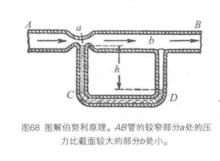
在图1中，向AB管吹进空气。如果管的切面小（像a处），空气的速度就大；而在切面大的地方（像b处），空气的速度就小。在速度大的地方压力小，速度小的地方压力大。因为a处的空气压力小，所以C管里的液体就上升；同时b处的比较大的空气压力使D管里的液体下降。

在图2中，T管固定在铁制的圆盘DD上，下面还有一个跟T管不相连的圆盘dd。空气从T管里出来以后，还要从两个圆盘之间间隙流出去，刚从T管里出来的空气流速很大，但是越接近盘边，空气的流速就越小，因为气流从两盘之间流出来，切面在迅速加大，但是圆盘四周的空气压力是很大的，因为这里的气流速度小；而圆盘之间的空气压力却很小，因为这里的气流速度大。因此图盘周围的空气对圆盘的压力较大，

周围空气的压力试图把两个圆盘推到一起；结果是，从T管里吹出的气流越强，圆盘dd被吸向圆盘DD的力也越大。

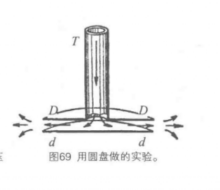
图3和图2相似，所不同的只是用了水。如果圆盘DD的边缘是向上弯曲的，那么在圆盘DD上迅速流动着的水会从原来比较低的水面自己上升到跟水槽里的静水面一般高。因此圆盘下面的静水就比圆盘上面的动水有更高的压强，结果就使圆盘上升。轴P的用途是不让圆盘向旁边移动。

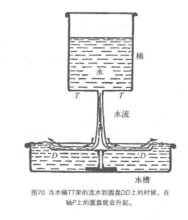
图4画的是一个飘浮在气流里的很轻的小球。气流冲击着小球，不让它落下来。当小球一跳出气流，周围的空气就会把它推回到气流里，因为周围的空气速度小，压力大，而气流里的空气速度大，压力小。

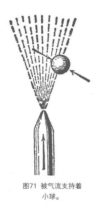
图5（a）中的两艘船在静水里并排航行着，或者是并排地停在流动着的水里。两艘船之间的水面比较窄，所以这里的水的流速就比两船外侧的水的流速高，压力比两船外侧的小。结果这两艘船就会被围着船的压力比较高的水挤在一起。海员们都知道，两艘并排驶着的船会互相强烈地吸引。

如果两艘船并排前进，而其中一艘稍微落后，像图5（b）所画的那样，那情况就会更加严重。使两艘船接近的两个力，会使船身转向，并且船B转向船A的力更大。在这种情况下，撞船是免不了的，因为舵已经来不及改变船的方向。

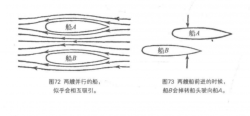
图5 两艘船并行。（a）两艘并行的船会相互吸引；（b）两船并行，一船稍微落后。

在图5中所说的这种现象，可以用下面的实验来说明。把两个很轻的橡皮球照图6那样吊着。如果你向两球中间吹气，它们就会彼此接近，并且互相碰撞。

伯努利

丹尼尔·伯努利[1] （1700年-1782年）出生于荷兰的格罗宁根，16岁时获艺术硕士学位，21岁时又获得医学博士学位。他曾申请解剖学和植物学教授职位，但未成功。

丹尼尔受父兄影响，一直很喜欢数学。1724年，他在去威尼斯的旅途中发表了《数学练习》一文，引起学术界关注，并被邀请到圣彼得堡科学院工作。1725年，25岁的丹尼尔受聘为圣彼得堡科学院生理学院士和数学院士。1727年，20岁的欧拉（后人将他与阿基米德、牛顿和高斯并列为数学史上的“四杰”）到圣彼得堡工作，成为丹尼尔的助手。

然而，丹尼尔不习惯圣彼得堡的生活，在8年以后的1733年，他找到机会返回巴塞尔，终于在那儿成为解剖学和植物学教授，后又成为物理学教授。

1734年，丹尼尔荣获巴黎科学院奖金，以后又10次获得该奖金。能与丹尼尔媲美的只有大数学家欧拉。丹尼尔和欧拉保持了近40年的学术通信，在科学史上留下了一段佳话。

在伯努利家族中，丹尼尔是涉及科学领域较多的人。他出版了经典著作《流体动力学》，研究了弹性弦的横向振动问题，提出了声音在空气中的传播规律。他的论著还涉及天文学、地球引力、潮汐、磁学、振动理论、船体航行的稳定和生理学内容等。博学的丹尼尔成为伯努利家族的代表人物。

丹尼尔于1747年当选为柏林科学院院士，1748年当选巴黎科学院院士，1750年当选英国皇家学会会员。

1782年3月17日，丹尼尔·伯努利在瑞士巴塞尔逝世，终年82岁。45

一次冲撞事件

1912年的秋天，当时世界上最大的轮船之一、远洋货轮“奥林匹克号”正在大海上航行。突然，一艘比它小得多的铁甲巡洋舰“豪克号”从后面追了上来，在离它100m的地方几乎跟它平行地疾驰。就在这时，一件意外的事情发生了：“豪克号”好像着了魔似的，竟然扭转船头朝“奥林匹克号”冲了过来，“豪克号”上的舵手怎么操作也没有用。结果，“奥林匹克号”无可奈何地接受了“豪克号”的亲密接触，并付出了极大的代价——船舷被“豪克号”撞了一个大洞。

在海事法庭审理这件奇案的时候，“奥林匹克号”的船长被判为有过失的一方，法院认为，这是因为他没有发出任何命令给横着撞过来的“豪克号”让路。船长虽然感到自己很冤枉，但没有办法解释，只好蒙冤受屈。案子就这样结束了，但这件事情却引起了一些科学家的注意，他们认为这次事件一定事出有因。

其实，早在1726年，丹尼尔·伯努利（1700-1782）就已经注意到：如果水沿着一条有宽有窄的沟（或粗细不均的管子）向前流动，沟的较窄部分就流得快些，但水流对沟壁的压力比较小；反之，在较宽的部分水就流得较慢，压向沟壁的力则会比较大。这一发现，后来被人们称为伯努利原理。

这个原理虽然发现得较早，但一直不被人们重视。出现了“奥林匹克号”被撞事件后，一些科学家突然想到，用这一原理来解释这次事故是非常合情合理的。于是，自此以后伯努利原理才渐渐得到了它应受的重视。这是一条普遍性的原理，它不仅对于流动的水是适用的，而且对于流动的其他液体甚至气体也适用。45

应用举例

球类比赛中的“旋转球”

球类比赛中的“旋转球”具有很大的威力。旋转球和不转球的飞行轨迹不同，是因为球的周围空气流动情况不同造成的。不转球水平向左运动时周同空气的流线。球的上方和下方流线对称，流速相同，上下不产生压强差。再考虑球的旋转，转动轴通过球心且平行于地面，球逆时针旋转。球旋转时会带动周同得空气跟着它一起旋转，致使球的下方空气的流速增大，上方的流速减小，球下方的流速大，压强小，上方的流速小，压强大。跟不转球相比，旋转球因为旋转而受到向下的力，飞行轨迹要向下弯曲。6

列车（地铁）站台的安全线

在列车（地铁）站台上都划有黄色安全线。这是因为列车高速驶来时，靠近列车车厢的空气被带动而快速运动起来，压强就减小，站台上的旅客若离列车过近，旅客身体前后会出现明显的压强差，身体后面较大的压力将把旅客推向列车而受到伤害。所以在火车（或者是大货车、大巴士）飞速而来时，旅客应站在安全线外规范等待。

船吸现象

当两艘船平行着向前航行时，在两艘船中间的水比外侧的水流得快，中间水对两船内侧的压强，也就比外侧对两船外侧的压强要小。于是，在外侧水的压力作用下，两船渐渐靠近，最后相撞。现在航海上把这种现象称为“船吸现象”。

刮风掀翻屋顶

当刮风时，屋顶上的空气流动得很快，而屋顶下的空气几乎是不流动的。根据伯努利原理，这时屋顶下气压大于屋顶上的气压。风速越快，屋顶上下的压力差越大，一旦风速超过一定程度，这个压力差就会导致屋顶被掀飞。

喷雾器

喷雾器是利用流速大、压强小的原理制成的。让空气从小孔迅速流出，小孔附近的压强小，容器里液面上的空气压强大，液体就沿小孔下边的细管升上来，从细管的上口流出后，液体受到空气流的冲击，被喷成雾状。

汽油发动机的化油器的原理与喷雾器原理相同。

离心式水泵

泵壳汇集从各叶片间被抛出的液体，这些液体在泵壳内顺着蜗壳形通道逐渐扩大的方向流动，流速逐渐减小，压力逐渐增大，流体的动能转化为静压能，减小能量损失。所以泵壳的作用不仅在于汇集液体，它更是一个能量转换装置。

文丘里流量计

文丘里流量计是测量流体压差的一种装置。它是一个先收缩而后逐渐扩大的管道。在收缩段的直管段截面1和截面2两处，测量静压差和两个截面的面积，并用伯努利方程即可计算出通过管道的流量。需要注意的是，由于收缩段的能量损失要比扩张段小得多，所以不能用扩张段的压强来计算流量，以免增大误差。