双曲线的标准方程

定义

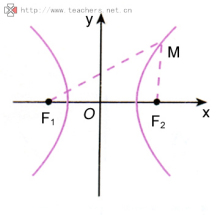设双曲线的焦距为2c，双曲线上任意一点到焦点F1，F2的距离的差的绝对值等于常数2a(c>a>0)2

以F1，F2所在直线为x轴，线段F1F2的垂直平分线为y轴，建立直角坐标系xOy，则F1，F2的坐标分别为（-c,0），（c,0）

设M（x,y）为双曲线上任意一点，根据双曲线定义知

|MF1-MF2|=2a

即| |=2a

化简得

因为

所以令 (b>0)得3：

两边除以 得 (a>0,b>0即焦点在x轴上)

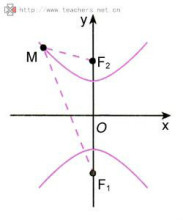类似可以得到焦点为F1（0,-c），F2（0,c）的双曲线的方程 (a>0,b>0即焦点在y轴上)

以上两种方程都叫做双曲线的标准方程4**。**

方程推导

推导双曲线标准方程的方法：移项平方法、直接平方法、分子有理化法、余弦定理法、平方差法。5

方程求解

求双曲线的标准方程主要是求实半轴长(a)和虚半轴长(b)。基本思路有两条途径：一是根据条件直接求得a与b的值；二是根据题设条件设出(a>0，b>0)标准方程，再建立关于a与b的方程组，进而求得a与b的值。6

1.直接法：就是不设出双曲线的标准方程，而是根据双曲线及相关圆锥曲线的几何性质等建立方程(组)直接求出a与 b的值。但是求解时，必须首先明确焦点在哪条坐标轴上。6

2.定义法：此方法主要适用于求动点的轨迹方程，解答时必须首先根据题设条件判定所求点的轨迹为双曲线，然后根据条件中的其他条件确定a、b的值，进而得到双曲线的标准方程，即为所求点的轨迹。6

3.待定系数法：就是根据题设条件设出所求的双曲线方程，然后建立方程或方程组求得参数.但在求解过程中，若能将条件与双曲线标准方程特征联系起来，巧妙设出相应的双曲线标准方程或变式方程，则可达到避繁就简的目的。6