中值定理

定义

函数与其导数是两个不同的函数；而导数只是反映函数在一点的局部特征；如果要了解函数在其定义域上的整体性态，就需要在导数及函数间建立起联系，微分中值定理就是这种作用。微分中值定理，包括罗尔定理、拉格朗日定理、柯西定理、泰勒定理。是沟通导数值与函数值之间的桥梁，是利用导数的局部性质推断函数的整体性质的工具。以罗尔定理、拉格朗日中值定理和柯西中值定理组成的一组中值定理是一整个微分学的理论基础。拉格朗日中值定理，建立了函数值与导数值之间的定量联系，因而可用中值定理通过导数去研究函数的性态；中值定理的主要作用在于理论分析和证明；同时由柯西中值定理还可导出一个求极限的洛必达法则。中值定理的应用主要是以中值定理为基础，应用导数判断函数上升，下降，取极值，凹形，凸形和拐点等项的重要性态。从而能把握住函数图象的各种几何特征。在极值问题上也有重要的实际应用。1

实际应用

微积分是与实际应用联系着发展起来的，它在天文学、力学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学等多个分支中，有越来越广泛的应用。特别是计算机的发明更有助于这些应用的不断发展。

客观世界的一切事物，小至粒子，大至宇宙，始终都在运动和变化着。因此在数学中引入了变量的概念后，就有可能把运动现象用数学来加以描述了。

由于函数概念的产生和运用的加深，也由于科学技术发展的需要，一门新的数学分支就继解析几何之后产生了，这就是微积分学。微积分学这门学科在数学发展中的地位是十分重要的，可以说它是继欧氏几何后，全部数学中的最大的一个创造。

相关概念

微分学

微积分学是微分学和积分学的总称。它是一种数学思想，‘无限细分’就是微分，‘无限求和’就是积分。十七世纪后半叶，牛顿和莱布尼茨完成了许多数学家都参加过准备的工作，分别独立地建立了微积分学。他们建立微积分的出发点是直观的无穷小量，但是理论基础是不牢固的。因为“无限”的概念是无法用已经拥有的代数公式进行演算，所以，直到十九世纪，柯西和维尔斯特拉斯建立了极限理论，康托尔等建立了严格的实数理论，这门学科才得以严密化。

微积分学基本定理指出，求不定积分与求导函数互为逆运算（把上下限代入不定积分即得到积分值，而微分则是导数值与自变量增量的乘积），这也是两种理论被统一成微积分学的原因。

极限

学习微积分学，首要的一步就是要理解到，“极限”引入的必要性：因为，代数是人们已经熟悉的概念，但是，代数无法处理“无限”的概念。所以为了要利用代数处理代表无限的量，于是精心构造了“极限”的概念。在“极限”的定义中，绕过了用一个数除以0的麻烦，而引入了一个过程任意小量。就是说，除数不是零，所以有意义，同时，这个过程小量可以取任意小，只要满足在Δ的区间内，都小于该任意小量，我们就说他的极限为该数。

应用

在一些等式的证明中，我们往往容易思维定式，只是对于原来的式子要从哪去证明，很不容易去联系其它，只从式子本身所表达的意思去证明。已知有这样一个推论，若函数 在区间I上可导，且连续，则 为I上的一个常量函数。它的几何意义为：斜率处处为0的曲线一定是平行于x轴的直线。这个推论的证明应用拉格朗日中值定理。

无穷小（大）量阶的比较时，看到两个无穷小（大）量之比的极限可能存在，也可能不存在。如果存在，其极限值也不尽相同。称两个无穷小量或两个无穷大量之比的极限为 型或 型不定式极限。解决这种极限的问题通常要用到洛比达法则。这是法则的内容，而在计算时往往都是直接的应用结论，没有注意到定理本身的证明，而这个定理的证明也应用到了中值定理2。

在一元函数微分学中，微分中值定理是应用函数的局部性质研究函数在区间上整体性质的重要工具，它在数学分析中占有重要的地位，其中拉格朗日中值定理是核心，罗尔定理是其特殊情况，柯西定理是其推广。拉格朗日微分中值定理有许多推广，这些推广有一些基本的特点，这就是把定理条件中可微性概念拓宽，然后推广微分中值表达公式。微分中值定理的应用为数学的进一步发展提供了广阔的天地。

类别

拉格朗日中值定理

中值定理是微积分学中的基本定理，由四部分组成。

内容是说一段连续光滑曲线中必然有一点，它的斜率与整段曲线平均斜率相同（严格的数学表达参见下文）。中值定理又称为微分学基本定理，拉格朗日定理，拉格朗日中值定理，以及有限改变量定理等。

如果函数 满足在闭区间[a,b]上连续；在开区间(a,b）内可导，那么在（a,b）内至少有一点 ，使等式 成立。

罗尔定理

如果函数 满足在闭区间[a,b]上连续；在开区间（a,b）内可导；在区间端点处的函数值相等，即 ，那么在（a,b）内至少有一点 ，使得 ；

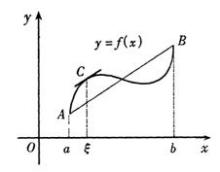
补充：几何上，罗尔定理的条件表示，曲线弧 （方程为）是一条连续的曲线弧，除端点外处处有不垂直于 轴的切线，且两端点的纵坐标相等。而定理结论表明，弧上至少有一点 ，曲线在该点切线是水平的。

柯西中值定理

如果函数 及 满足:

⑴在闭区间[a,b]上连续；

⑵在开区间（a,b）内可导；

⑶对任一x属于(a,b），F'(x)不等于0

那么在（a,b) 内至少有一点 ，使等式 成立。也叫Cauchy中值定理。

若令u=f(x),v=g(x），这个形式可理解为参数方程，而 则是连接参数曲线的端点斜率， 表示曲线上某点处的切线斜率，在定理的条件下，可理解如下：用参数方程表示的曲线上至少有一点，它的切线平行于两端点所在的弦，这一点Lagrange也具有，但是Cauchy中值定理除了适用y=f(x）表示的曲线，还适用于参数方程表示的曲线。

当柯西中值定理中的g(x)=x时，柯西中值定理就是拉格朗日中值定理。3

积分中值定理

f(x）在a到b上的积分等于 ），其中c满足a<c<b.

如果函数 f(x) 在积分区间[a, b]上连续，则在 [a, b]上至少存在一个点 ξ，使下式成立

其中(a≤ξ≤b)。4

发展

17 世纪由牛顿和莱布尼茨创立的微积分 , 为数学的研究提供了强有力的工具。此后的大部分数学家的注意力都被这有着无限发展前途的学科所吸引。从此有了数学家们对微积分的研究。在微积分建立之前，人们就开始对微分中值定理进行了研究。6

早在 1637 年 ,法国著名数学家 Fermat 在一文《求最大值和最小值的方法》中首次给出了费马定理。6

在 1691 年，法国著名数学家 Rolle 在一文《方程的解法》中首次给出了多项式形式的罗尔中值定理。6

在 1797 年 , 法国伟大的数学家 Lagrange 在一书《解析函数论》中首次给出了拉格朗日中值定理 , 并给出了其原始的证明。6

但真正意义上系统研究微分中值定理的是法国伟大的数学家 Cauchy,他给出了数学分析理论的严格化 , 他的三部旷世巨著《分析教程》,《无穷小计算教程概论》(1823 年 ),《微分计算教程》(1829 年 ), 进行了严格化定义 , 重构了微积分理论。他首先阐述了微分中值定理的重要作用 ,使其成为微分学的核心定理。6

在《无穷小计算教程概论》一文中 ,Cauchy 首先对拉格朗日定理进行了严格的证明 , 又在《微分计算教程》一文中将拉格朗日定理推广为柯西中值定理。因此发现了最后一个漂亮的微分中值定理。6

罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理在逻辑上是等价的。但在形式上，拉格朗日中值定理、柯西中值定理和泰勒定理都是罗尔定理的推广，柯西中值定理和泰勒中值定理同时也是拉格朗日中值定理的推广。罗尔定理就是导数的零点定理。这些中值定理中，以罗尔定理、拉格朗日中值定理和泰勒定理出现数学考题最多。5