近轴光线

定义

入射到近轴球面上并与光轴（z 轴）的夹角很小的光线称为近轴光线。

设近轴光线与光轴的夹角为 ，则 。（因为是近轴光线，α角很小，趋近于0。另外，通过光学系统之后，近轴光线可认为交于一点）

近轴光线是一种物理模型。是指可以用斯涅耳折射定理（光的折射定律）来描述的光线。这一类光线离主光轴的距离可以认为是0。它可以把问题简化，因此是一种常用的模型。1

符号规则

设在空间存在如下一个折射球面：

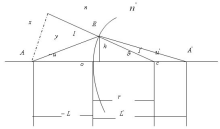
r：折射球面曲率半径；o：顶点；L：物方截距；L'：像方截距；u：物方孔径角；u'：像方孔径角；

符号规则：光线方向自左向右

（1） 沿轴线段：以顶点O为原点，光线到光轴交点或球心，顺光线为正，逆光线为负。

（2） 垂轴线端：光轴以上为正，光轴以下为负。

（3） 光线与光轴夹角：由光轴转向光线锐角，顺时针为正，逆时针为负。

（4） 光线与折射面法线的夹角：由光线经锐角转向法线，顺时针为正，逆时针为负。

（5） 光轴与光线的夹角：有光轴经锐角转向法线，顺时针为正逆时针为负。

（6） 折射面间隔：d有前一面顶点到后一面顶点方向，顺光线方向为正，逆光线方向为负。2

光路计算

公式：

由（1）、（2）、（3）、（4）推出

（5）式说明：在近轴区l’只是l的函数，它不随孔径u的变化而变化，轴上物点在近轴区成完善像，这个像点称高斯像点。

高斯像面：通过高斯像点且垂直于光轴的平面称为高斯像面。

共轭点：像上面提到的一对构成物象关系的点称为共轭点。

在近轴区有：

由公式(1)(2)(3)(4)(5)(6)可推出：

4

(7)式中Q称为阿贝不变量，对于单个折射球面物空间与像空间的Q相等；

(8)式表明了物、像孔径角的关系

(9)式表明了物、像位置关系

限制了光线与光轴的夹角,光线在折射面上 的入射角,折射角等都很小.所有角度小于5°正切,正弦都可用该角度的弧度值代替。

近轴范围

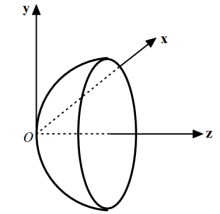
在光学系统的近轴范围内，其折射面或反射面的面形可以由下式表示：

现以球面为例看看这个近轴球面定义的实质，由球面方程考查比较。如果h与r相比很小，允许取近似。则有

其中，，即在近轴范围里，允许作这种近似。它是一个近轴球面，h远小于近轴球面半径r。

列矩阵表示

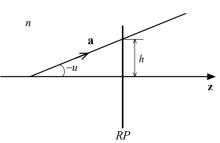
含光轴面(纸面)内的任一近轴光线可用该光线在参考面上的投射高度h，以及它与光轴的夹角μ（即孔径角）这两个参数来表示。又为了表明该光线所在的媒质折射率n，将n与μ的乘积nμ作为一个参数，称谓光学方向余弦。这样，光线可用列矩阵a表示，即

近轴光线的折射矩阵

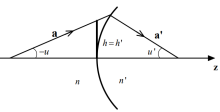
如图1所示是一个近轴折射球面，两边媒质的折射率分别为n和n’，近轴球面半径为r。近轴光线，入射到这个近轴球面上，经其折射成为折射光线。

将参考面取在过近轴球面顶点的切平面上，由近轴光线的性质知，如下关系成立h'=h。

近轴光线在近轴球面上折射前后满足关系：

两式联立并写成矩阵形式有：

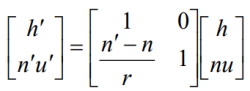
方阵只含有近轴球面系统的参量。称其为近轴光线的折射矩阵，用R简记之 ，即3

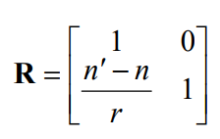
应用

近轴光线一般被应用于高斯光学。几何光学中研究和讨论光学系统理想成像性质的分支称为高斯光学（或近轴光学）。它通常只讨论对某一轴线(即光轴)具有旋转对称性的光学系统。