周期信号

信号分类

常见的周期信号有：正弦信号、脉冲信号以及它们的整流、微分、积分等。这类可称为简单信号。它们的特点是在一个周期内的极值点不会超过两个且周期性特征明显。对于这类已明确具有周期特性的信号，周期与否的判别相对简单，周期测量的方法也很成熟完善，如：过零检测法，脉冲整形法等

表达式

x（t）=x（t+kT），k=1，2......

式中t表示时间，T表示周期。

信号划分

一个信号既可以是模拟的也可以是数字的。如果它是连续时间和连续值，那么它就是一个模拟信号。如果它是离散时间和离散值，那么它就是一种数字信号。除了这种区分外，信号也可以分为周期性的或非周期性的。周期性信号是一种经过一定时间重复本身的，而非周期性信号则不会重复。模拟和数字信号既可以是周期性的也可以是非周期性的。1

区别周期信号和非周期信号的方法：1、周期信号的频谱是离散的，准周期信号的频谱是连续的。2、因周期信号可以用一组整数倍频率的三角函数表示，所以在频域里是离散的频率点。准周期信号做Fourier变换的时候，n趋向于无穷，所以在频谱上就变成连续的了。2

周期性计算

试判断下列各信号f(t)是否为周期信号。若是，其周期T为多少？2

（1）f(t)=cos2t+sin3t

（2）

（3）f(t)=10cos4πtU(t)

解

(1) f(t)为两个子信号f1(t)=cos2t与f2(t)=sin3t的和，即f(t)=f1(t)+f2(t)，且f1(t)=f1(t-n1T1),f2(t)=f2(t-n2T2)，其中n1∈Z，n2∈Z。则当T1/T2=n2/n1(n1与n2必须为不可约的整数)时，f(t)即为周期信号，其周期T=n1T1=n2T2。

今子信号cos2t的周期为πs，子信号sin3t的周期为2π/3s。故有T1/T2=3/2

由于3/2已为不能再约的整数比，故f(t)为周期信号，其周期T为2πs.

(2) 因f(t)的振幅是随时间按指数规律变化的，故f(t)不是周期信号。

(3) 因f(t)不是无始无终的信号，而是有始无终的信号，故不是周期信号。

matlab程序

在数字信号处理中，有四种傅里叶变换，如果时域是周期的，则变换域一定是离散(谱线)的。如果频域具有周期性，则时域一定是离散的。

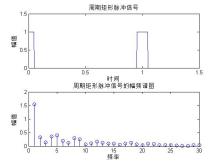
矩形信频谱

fs=150;N=200; %采样频率为150Hz，点数为200点

Dt=1/fs;%数字角频率

t=(0:N-1)*Dt;

A=1;P=2*pi;

y=A*square(P*(t+0.05),10); %周期脉冲函数

subplot(2,1,1)

plot(t,y); %周期脉冲波形

axis([0 1.5 0 1.5])

xlabel('时间')

ylabel('幅值')

title('周期矩形脉冲信号')

Y=fft(y); %快速傅里叶变换

fy=(abs(Y)*2)/N; %频谱

subplot(2,1,2)

stem(fy);

axis([0 30 0 2])

xlabel('频率')

ylabel('幅值')

title('周期矩形脉冲信号的幅频谱图')