动植物也懂斐波那契数列？这是大自然进化的“隐藏技能”吗？

一般来说，“高小”毕业的学生也大概听说过斐波那契数列这个数学问题。那么，这个数学问题怎么和生物力学扯上了关系呢？还很“美”？！

在很长一段时间里，数学和力学其实是不分家的，现在也是“若即若离”“藕断丝连”的状态。扯远啦！我们还是重点介绍斐波那契数列的生物力学之美，到底有多美。

一、什么是斐波那契数列？

1.斐波那契数列的定义与生成规则

斐波那契数列最初由中世纪意大利的数学家列昂纳多·斐波那契(1175-1250)在研究兔子生崽的问题时发现的现象和规律。如果每对兔子（一雄一雌）每月能生殖一对小兔子（假设也是一雄一雌，下同），且兔子在出生两个月后，就有繁殖能力，如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？我们不妨拿新出生的一对小兔子来分析一下。从图1可以看出兔子随着月份增加而长大并繁殖的情况。

图1 兔子随着月份增加而长大并繁殖的情况

最后兔子的总对数形成这样一个数列：1、1、2、3、5、8、13、21……这便是斐波那契数列，也叫“兔子数列”。这个数列的生成规则是：从第三项开始，每一项都是数列中前两项之和，比如：2=1+1，3=1+2，5=2+3，8=3+5……

2.斐波那契数列与黄金分割的关系

黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值约为0.618（如图2所示），而这个数的倒数是1.618，是不是完美的巧合？这个比例被公认为是最能引起美感的比例，因此被称为黄金分割（在英文里，“黄金XX”往往用来形容XX完美、权威的含义）。它经常出现在自然界和艺术中，被认为是美的象征。

图2 黄金分割线

现在，让我们来看看斐波那契数列与黄金分割之间的关系。这里有个非常有趣的现象。如果取斐波那契数列中相邻两个数的比值，那么就会发现：随着项数的不断增加，前一项与后一项比值会越来越接近黄金分割比。具体来说，当我们在斐波那契数列中取较大的两个连续的数字并计算它们的比值时，这个比值会趋近于黄金分割比。例如，21/34 ≈ 0.6176，89/144=0.6181，这已经非常接近黄金分割比了。因此，斐波那契数列也被称为黄金分割数列。

大家都是“识数”的人，认识这个数，又有何意义？

举个“栗子”：与黄金分割有关的几何图形有“黄金矩形”和“黄金螺线”。黄金矩形的长宽之比为黄金分割率；亦即，矩形的短边为长边的 0.618倍。在黄金矩形里靠着三边做成一个正方形，剩下的那部分则又是一个黄金矩形。可以依次再做成正方形和黄金矩形，周而复始（图3左）……

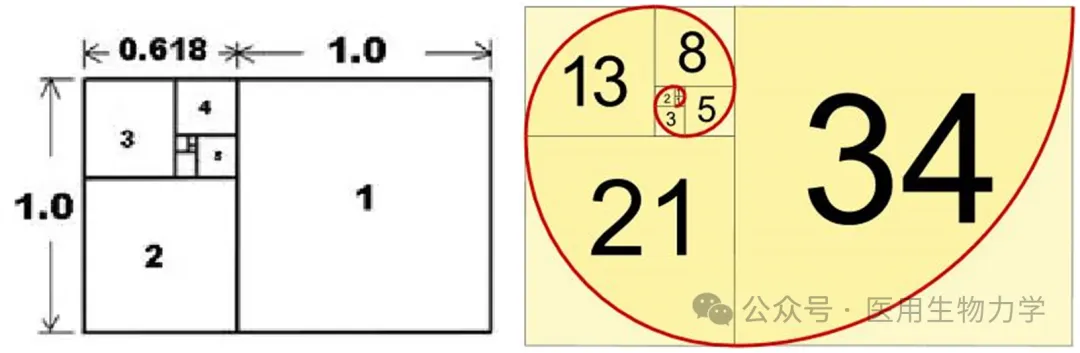
图3 黄金矩形（左）和黄金螺线（右）

黄金螺线，也称斐波那契螺旋线，是根据斐波那契数列画出来的螺旋线。它是这样做出来的：在以斐波那契数为边的正方形拼成的长方形（即黄金矩形）中画一个90度的扇形，连起来的弧线就是斐波那契螺旋线（图3右）。自然界中存在许多斐波那契螺旋线的结构（图4），满足最完美的黄金比例，这是大自然的精妙设计。在生物学中，许多动植物的生长过程都遵循着斐波那契数列的规律，如花瓣的数量、菠萝表面的鳞片排列等。这种现象被称为“斐波那契现象”，是自然界中普遍存在的一种规律。

图4 自然界的各种斐波那契螺旋线结构

这些动植物为什么会选择斐波那契数列作为它们的“设计蓝图”呢？这背后又隐藏着怎样的科学机理呢？这么巧，那么美，一定有道理。

3.斐波那契数列在数学和其他领域的应用

在数学领域，斐波那契数列的应用非常广泛。这种黄金分割的性质使得斐波那契数列在几何学和艺术领域有着广泛的应用，例如在建筑设计、绘画和雕塑中都可以看到黄金分割比的影子。除此之外，斐波那契数列还在代数学、组合数学和数论等领域有着重要的应用。例如，在代数学中，斐波那契数列的通项公式是“递归算法”的经典例子。

在组合数学中，许多组合问题都可以转化为斐波那契数列的求解问题。在数论中，研究斐波那契数列中的素数分布、斐波那契数列的模运算性质等。

在计算机科学中，斐波那契数列可以用于实现高效的查找和排序算法，如斐波那契查找和斐波那契排序。同时，斐波那契数列也在密码学、数据压缩等领域有着广泛的应用。

在金融领域，斐波那契数列也被用来分析股票价格和市场趋势。斐波那契回撤水平是一种流行的技术分析工具，用于确定价格可能反弹或反转的点位。

如果细说，那就是一个长长的列表。在此就像风一样先掠（略）过。下面说生物力学主题。

二、斐波那契数列的生物力学之美

自然界中的斐波那契数列是一种令人惊叹的现象。道理在哪里？生物力学里。

先认识一个概念——形态学。

形态学是研究生物体外部形态和结构的学科，它关注生物体如何通过其形态来适应环境和实现其功能。从生物力学的角度来看，动植物选择斐波那契数列作为其形态学特征的基础，可能是因为它们在长期的自然选择过程中发现，这样的结构能够更好地适应环境，提高生存和繁殖的成功率。这是生存竞争、优化的结果。可以被理解为一种优化策略，这种策略有助于生物体在生长、发展和适应环境方面实现最佳效果。当然，这只是笼统地说说大道理。下面具体解释详细的小道理。从形态学的角度来看，稳定性和适应性是生物体形态与功能紧密相连的两个关键方面。

稳定性是指生物体在面对外部扰动时能够保持其形态和结构不变的能力。在形态学上，稳定性通常与生物体的结构强度和刚度有关。

适应性是指生物体能够根据其生活环境和需求而调整其形态和结构的能力，以增加生存和繁殖的机会。

在形态学上，适应性表现为生物体的形态和结构与其生存环境之间的匹配。

（1）从强度的角度分析斐波那契数列的力学问题

通过采用斐波那契数列的形态，生物体能够以一种高效和最优的方式利用空间和资源，同时保持结构的稳定性。例如，树木的树枝和树叶的分叉方式符合斐波那契数列（图5中的树枝长度和直径等几何参数），树木的枝干通过其粗壮的基部和分支结构来抵抗风力和重力的作用，从而保持整体的稳定性。

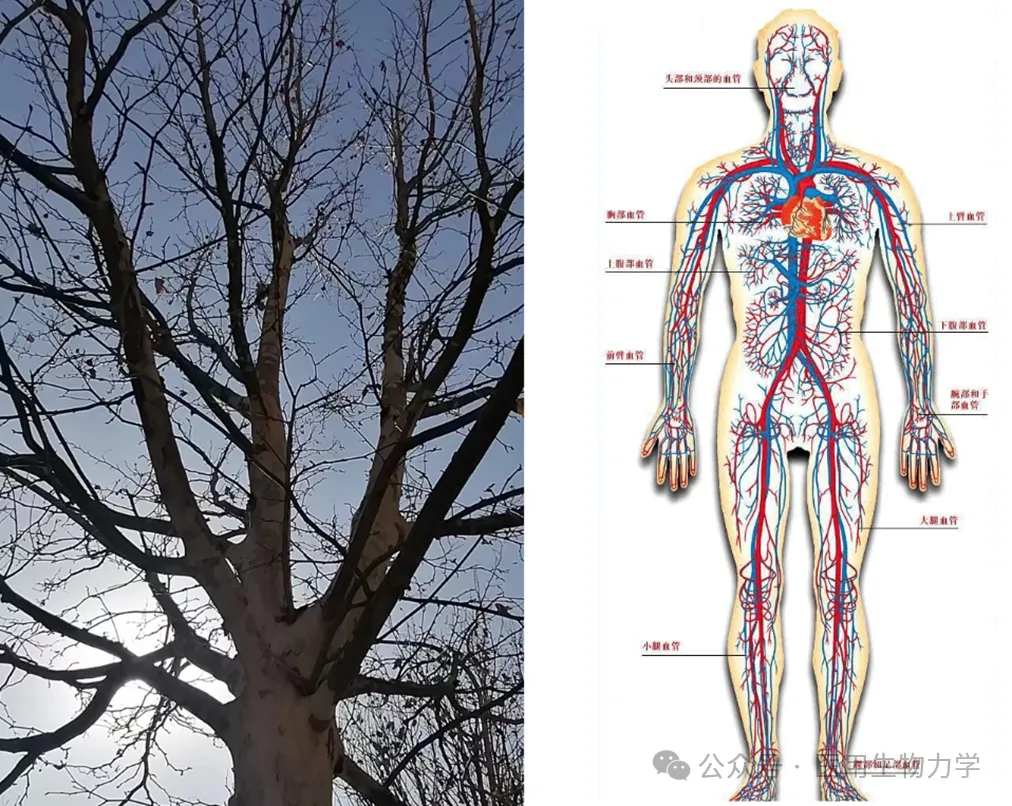
图5 树枝的形态（左）和人体血管树的形态（右）

通过模拟风力对植物结构的受力分析，可以研究斐波那契数列对植物结构稳定性的影响。为了简化而又能说明白道理，我们把树枝模拟为悬臂梁进行受力分析（图6）。不管是受到集中力或者均布力的风力作用，悬臂梁（树枝）所承受的弯矩都是根部最大、末梢最小；如果悬臂梁的截面大小是均等的，那么由此而产生的应力分布也是根部最大、末梢最小，后果就是根部很容易因为受力大、强度不足而折断。为了避免这种情况发生，树枝根部的直径都比较粗大，从根到梢的直径逐步减小。树枝都是这么长的，这也是大家容易理解的。这是从强度的角度分析斐波那契数列的力学问题。

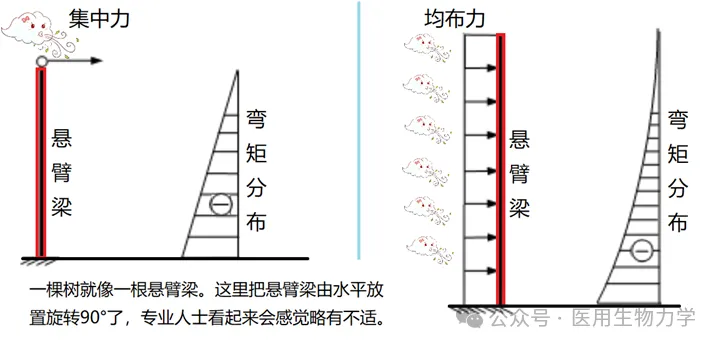
图6 把树枝模拟为悬臂梁进行受力分析

从受力分析的角度来看，斐波那契数列在自然界中的广泛应用也有其合理之处。这种稳定性不仅有助于树木在恶劣环境中的生存，还为其提供了稳定的支撑，使其能够向上生长并展开枝叶以进行光合作用。

那位看官说了，树枝并不都是长成这个样子啊？！没错，树枝形态还会受到其他因素（如材料、外部环境等）影响。这里不展开论述。与树枝的形貌类似，人体循环系统中的血管树也有类似树枝的形态，这其中也受到生物力学原理（如莫里法则、等切应力原理等）的作用。也按下不表，继续分析斐波那契数列。

在动植物中，许多结构都呈现出斐波那契螺旋形态，如向日葵的花瓣、松果的鳞片、海螺的壳等。这些螺旋形态不仅美观，而且具有极强的结构稳定性。斐波那契数列的特性使得这些螺旋形态在生长过程中能够保持稳定的形态，同时有效地分散外部力的作用，从而增强生物体的生存能力。

现在，让我们想象一个简化的向日葵花瓣受力分析模型。假设每片花瓣都受到两个主要力的作用：一个是来自花茎的支撑力，另一个是来自相邻花瓣的挤压力。在理想情况下，如果每片花瓣受到的力都是均匀的，那么整个花朵的结构就会非常稳定。斐波那契数列在这里发挥作用的方式是，它通过影响花瓣的数量和排列，间接地影响了每片花瓣受到的力。由于斐波那契数列的特性，相邻两片花瓣之间的角度（如果我们把花瓣看作是围绕花中心排列的点）是逐渐变化的，并且这种变化遵循一种特定的规律。这种规律确保了每片花瓣都有足够的空间来生长，同时也保证了整个花朵的结构稳定性。具体来说，当外部力（如风或昆虫的触碰）作用于花朵时，这种力会沿着花瓣的螺旋排列方向分散开来。由于斐波那契数列的特性，这种力的分散是非常均匀的，没有哪个部分会受到过多的压力或拉力。这就好像是在一个紧密排列的军队中，每个士兵都能够均匀地分担来自外部的压力，从而保持整个队伍的稳定性。

有兴趣和能力的小伙伴，可以尝试用结构拓朴优化设计的方法来算一下向日葵葵花籽的形态为什么是菱形而且呈斐波那契螺旋的形态分布。从数学和力学角度优化后的结果，就是我们看到的向日葵的真实形貌。

（2）从刚度的角度分析斐波那契数列的力学问题

树叶的叶脉分布也经常呈现出黄金比例。大连理工大学郭旭教授团队针对自然界中树叶叶脉黄金比例分布之谜开展了深入研究。他们基于结构拓扑优化理论的仿生研究，探求使得树叶刚度最大化的叶脉分布构型（图7）。

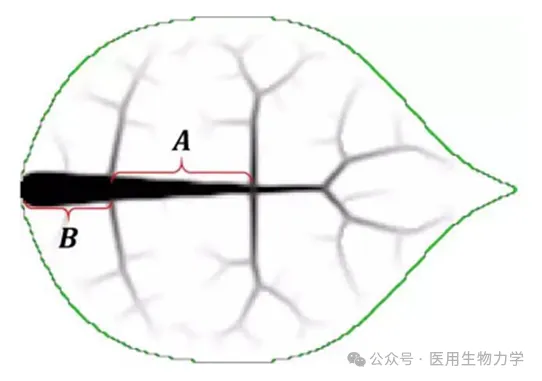
图7 典型树叶的最优叶脉分布构型

研究发现叶脉主干首段与次段（A/B）呈现近似黄金比例分布时，树叶的结构刚度最大，即树叶变形最小，从而使其具有最大的等效光照面积，提高叶肉组织的光合作用效率。上述结果初步证实了树叶叶脉分布是力学性能最优化驱动下的演化结果。该研究结果不仅可以解释叶脉分布的奥秘，而且为设计天线、柔性电子器件等加筋板壳结构的设计提供了很有借鉴意义的指导原则。

（3）动物的斐波那契数列

许多动物的骨骼和肌肉结构也呈现出与斐波那契数列相似的分级分叉形态，这种形态不仅可以提高动物的运动效率，还能够有效地保护它们免受外界伤害。海螺的壳呈现出一种对数螺旋的形态（图8左），这种形态不仅美观，而且具有极强的结构稳定性。在受到外力冲击时，这种对数螺旋的结构能够有效地分散冲击力，保护海螺内部的软组织不受伤害。

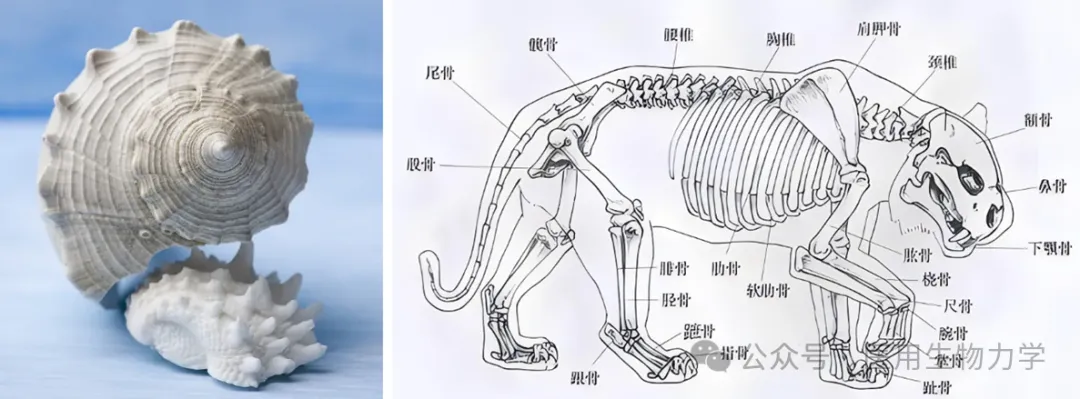
图8 海螺（左）和猫科动物（右）中的斐波那契数列

动物的四肢骨骼和肌肉结构可能也受到斐波那契数列的影响。例如，研究显示，猫科动物的四肢骨骼长度比接近斐波那契数列（图8右），这种结构可能有助于提高动物的运动效率和稳定性。通过模拟动物运动过程中的受力情况，可以研究斐波那契数列对动物运动稳定性的影响，有助于它们在生存和竞争中保持优势。生物组织的生长过程可能也遵循斐波那契数列。例如，研究表明，某些细胞分裂方式可能遵循斐波那契数列，这种生长模式可能有助于维持组织结构的稳定（就像兔子下小兔子的数列一样）。通过模拟细胞分裂过程中的受力情况，可以研究斐波那契数列对生物组织生长稳定性的影响。

（4）从最小作用量原理的角度来理解斐波那契数列的稳定性

最小作用量原理是物理学中的一个基本原理，也被称为哈密顿原理，是经典力学中的一个基本原理。它指出在自然界中，物理系统的演化总是遵循使得作用量达到极小的路径。在静态或平衡态的情况下，这一原理与势能最低原理是密切相关的，因为系统往往会寻求势能最小的状态，这是一种稳定的状态。

在生物形态学中，这个原理可以被解释为生物体在进化过程中会选择一种能够最小化能量消耗、最大化资源利用和应对环境挑战的形态策略。例如，向日葵花瓣按照斐波那契数列的螺旋状方式排列，这样的排列方式可能使得花朵在开放时能够最大程度地展开，同时保持结构的稳定性。这种稳定性有助于保护花朵免受外部损伤，同时也使得花朵能够更加有效地进行光合作用。又如，树木的分支结构、动物的骨骼形态等都可以通过减少弯曲和扭曲来降低势能，从而增加稳定性。还有如松果的鳞片、鹦鹉螺的壳等结构都表现出一种优美的螺旋形态，这种形态可能是通过最小化能量消耗和最大化结构稳定性来演化的。

（5）从最小作用量原理的角度来理解斐波那契数列的适应性

许多生物体的形态和结构呈现出斐波那契数列的特点，如花瓣的数量、松果的鳞片排列等。这种数列的特点在于其相邻两项之比逐渐逼近黄金分割比，这使得形态在视觉上更加和谐。这种外观的和谐之美不是目的，根本的生物力学之美才是原因。事实上，这种斐波那契数列的排列方式是一种空间填充策略，它允许花瓣在有限的空间内以最大化的方式展开，从而最大化地接受阳光和进行光合作用，有助于植物在生长和发育过程中能够以最有效的方式利用空间和资源，从而提高生存和繁殖的机会。因此，斐波那契数列在形态学上的体现可以被视为一种适应性策略。

三、小结

斐波那契数列与自然界之间确实存在着一种神秘而有趣的联系。这种联系不仅展示了数学的魅力，也揭示了自然界中隐藏的力学奥秘。从生物力学的角度来看，斐波那契数列在自然界中的出现可以被理解为一种优化策略，这种策略有助于生物体在生长、发展和适应环境方面实现最佳效果。这种数列的特性使得生物体能够以最有效的方式利用空间和资源，保持稳定的形态，同时有效地分散外部力的作用，从而增强生物体的适应性和生存能力。

当然，我们目前对斐波那契数列与自然界关系的理解还只是冰山一角，未来还有更多的科学问题需要我们去探索和解答。期待各界朋友提出更有趣的问题、提供更专业的解读、揭示更精彩的发现。