“讨价还价”也有博弈论模型！

讨价还价是市场经济中最常见、最普通的事情，也是一种典型的消耗战。我们将通过对讨价还价博弈的分析来揭示消耗战的一般特点。

讨价还价博弈假设有两人就如何分享1笔钱进行谈判，规则如下:

甲乙轮流做决策。甲给出分配方案S1，即自己得S1，乙获得1-S1。乙可以接受，或者拒绝，若乙拒绝，则由乙提出新的分配方案。博弈按此规则不断循环进行，直至其中任何一方接受对方的方案，博弈宣告结束。被拒绝的方案对以后的博弈阶段没有影响。由于谈判费用和利息损失等，讨价还价每多进行一个阶段，博弈双方的利益就会有一定损失，二人的贴现率相同，贴现因子均为δ，即博弈每多进行一个阶段，参与者所得利益需乘以δ。

为了简化问题，先讨论一个只有三阶段的讨价还价，即博弈进行到第三阶段时乙必须接受甲的方案--无论结果如何。具体来说，博弈过程如下。

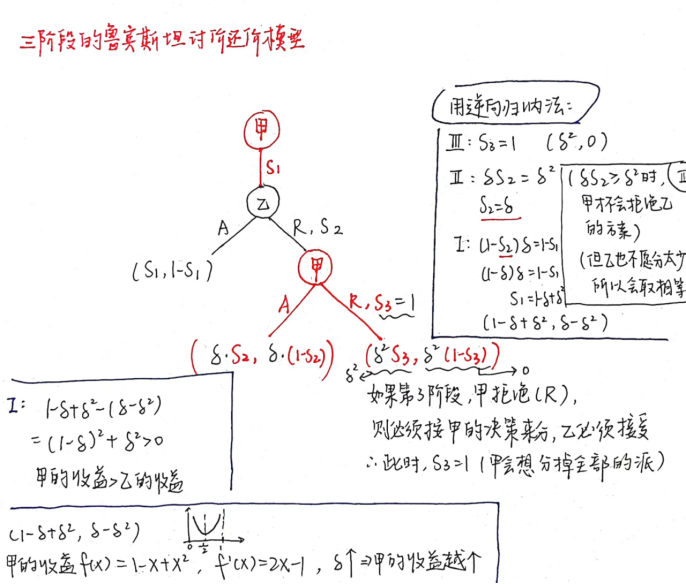
综上所述，子博弈完美纳什均衡所对应的路径为：甲在第一阶段出价1-δ+δ^2，乙接受δ-δ^2。

进一步讨论该博弈的均衡结果，可以发现，当贴现率越高时，甲的收益越高。这种结果反映了在此博弈中乙赖以讨价还价的筹码就是可以跟甲耗时间。换言之，虽然最终甲可以争得全部利益，但拖延时间会给甲带来损失。损失越大，耐心越小，则甲愿意分给乙的利益就越大。

上述博弈问题及其结果，在现实生活中有许多例子，如利润分配、债务纠纷、商品交易等，都可以是这个博弈模型的原型。该模型的第一、第二阶段相当于纠纷或争执的各方以不同形式的调解过程，而第三阶段则相当于最后由仲裁机构或第三方进行裁决。模型中的折现因子δ则显示相关各方花费在谈判和诉讼等方面的时间、金钱等代价。

参考文献：

[1]葛泽慧,于艾琳,赵瑞,赵世豪.博弈论入门[M].清华大学出版社：2018.