扩展式博弈

本次将为大家介绍扩展式博弈。在分析扩展式博弈时，我们通常会用到“博弈树”，博弈树是通过节点和分支来分析博弈的工具

首先我们通过“阻吓博弈”的例子介绍如何使用博弈树进行分析。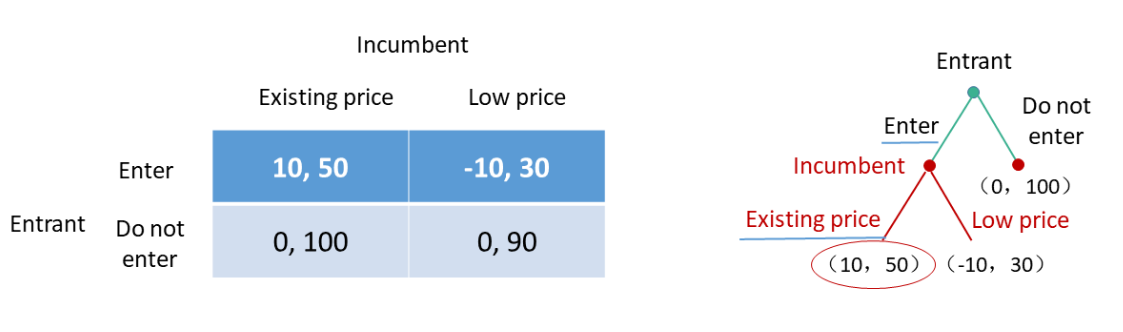

现在市场上只有一家企业（incumbent），另一家企业可以选择是否入场，如果选择入场，对于旧企业而言，如果选择保持价格，那么新企业获得10收益，旧企业获得50收益；如果选择降低价格打价格战，那么新企业获得10亏损，旧企业获得30收益；如果选择不入场，对于旧企业而言，如果保持价格，那么旧企业获得100收益，如果降低价格，则旧企业获得90收益，而新企业无论如何都不会获得收益。但新企业如果不入场，旧企业就不会选择降价，所以在博弈树上，新企业的“do not enter”下没有多的分支。

与该博弈类似的还有“协调博弈”，即每个参与者的收益取决于他们与对方的协调程度，如果选择同样的策略，双方获得相同的收益，如果选择了不同的收益，那么双方获得相同的亏损，博弈的目的是使每位参与者的收益最大化。而该博弈中可能存在多个纳什均衡。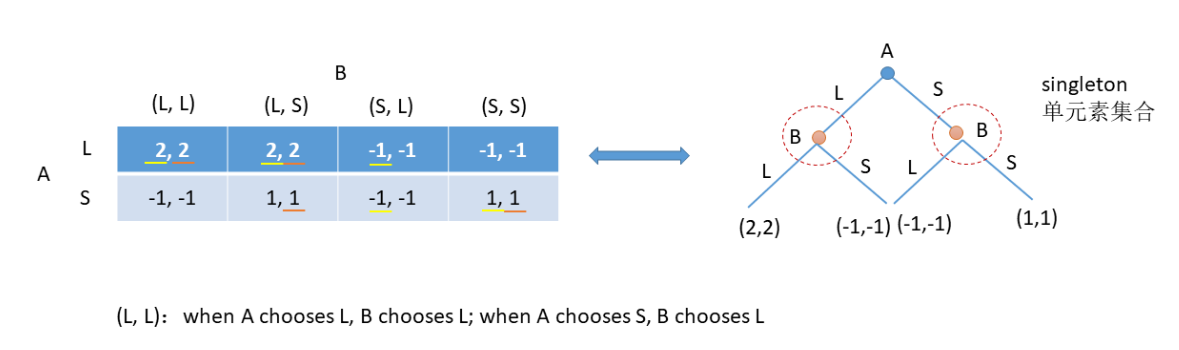

这里要特别解释一下表格中对策略的描述：（L,L）是指，第一个L对应A的第一个策略，当A选择L时，那么B选择第一个策略，当A选择S时，那么B选择第二个策略，例如：（S,L）：A选择L时，B选择S，A选择S时，B选择L。由此我们根据右边的博弈树，得到左边的收益表格。利用画线法可以得到三个均衡，分别是：A选L时B选L；A选L时B选L；A选S时B选S。与协调博弈的要求相符。

当对博弈树分析纳什均衡时，可以采用“逆向归纳”法：

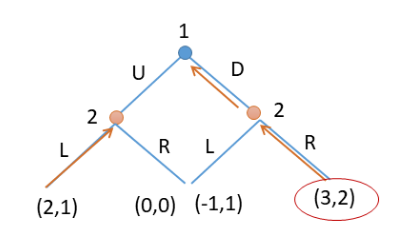
从最终的结果开始分析，倒推回最初的策略。举图片中的例子：对于所有的结果，由于最后一步由2决定，那么就要比较2的收益。在左边的分支中，（2，1）和（0，0）相比，1大于0，那么选择（2，1），在分支上画一个倒回的箭头，右侧同理选择（3，2），此时回到第一步，也即1的选择，此时比较1的收益大小，（2，1）和（3，2）中3大于2，则选择（3，2），在右侧画一个倒推回的箭头指向最初的1，综上，最终得到的纳什均衡为（3，2）。

另一种扩展式博弈是重复博弈，参与者重复进行同一种博弈，最终每次博弈的收益是所有收益的的加权平均数。对于重复博弈来说，可以是静态博弈，也可以是动态博弈，但整体而言是动态博弈，后一次博弈不会受到前一次博弈的影响，每一次博弈的规则、策略等均完全相同。