自由能原理（上）：生命、意识与智能的统一原理

导语

自由能原理被认为是“自达尔文自然选择理论后最包罗万象的思想”，从第一性原理出发解释智能体更新认知、探索和改变世界的机制，被认为有可能成为智能的第一性原理的重要候选方案，并有望成为新时代复杂系统的大统一理论。本文是对自由能原理的概览介绍文章，欢迎开启这趟自由能之旅，探讨智能的第一性原理！

关键词：自由能原理，主动推理，贝叶斯定理，生成模型，随机动力系统，马尔可夫毯

作者｜牟牧云

编辑｜梁金

目录

1. 生命、意识与智能的统一原理

2. 主动推理的底层路径：从贝叶斯定理出发

3. 主动推理的顶层路径：从随机动力系统出发

从微小的细菌到复杂的动物，包括人类，都可以被看作是具有某种形式智能的存在。例如，培养皿中的细菌能够通过细胞膜上的受体蛋白来检测环境中化学物质的浓度梯度，并通过化学趋向性这一过程，向有利的化学物质浓度方向移动，同时避开有害物质。细菌这种单细胞生物，尽管结构简单，却具备了感知环境和做出行动的基本能力，这使得它们能够寻找食物或逃避危险。

当许多单细胞生物通过简单行为进行交互汇聚成多细胞生物时，我们便见证了更为丰富和复杂的智能行为的诞生。以人类大脑为例，它由大约1000亿个神经元组成，这些神经元通过约100万亿个连接形成了一个庞大而复杂的网络，共同构成了我们对世界的感知，控制身体运动，还赋予了我们意识、思考、学习和记忆的能力。

从单细胞生物的适应性行为，到多细胞生物复杂神经元网络所孕育的智能行为，我们不禁好奇：这些现象之间是否存在一种普遍适用的原理？自由能原理（Free Energy Principle）及其衍生的主动推理（Acitive Inference，也译作主动推断）框架，尝试从第一性原理出发，为我们提供一个可能的答案。

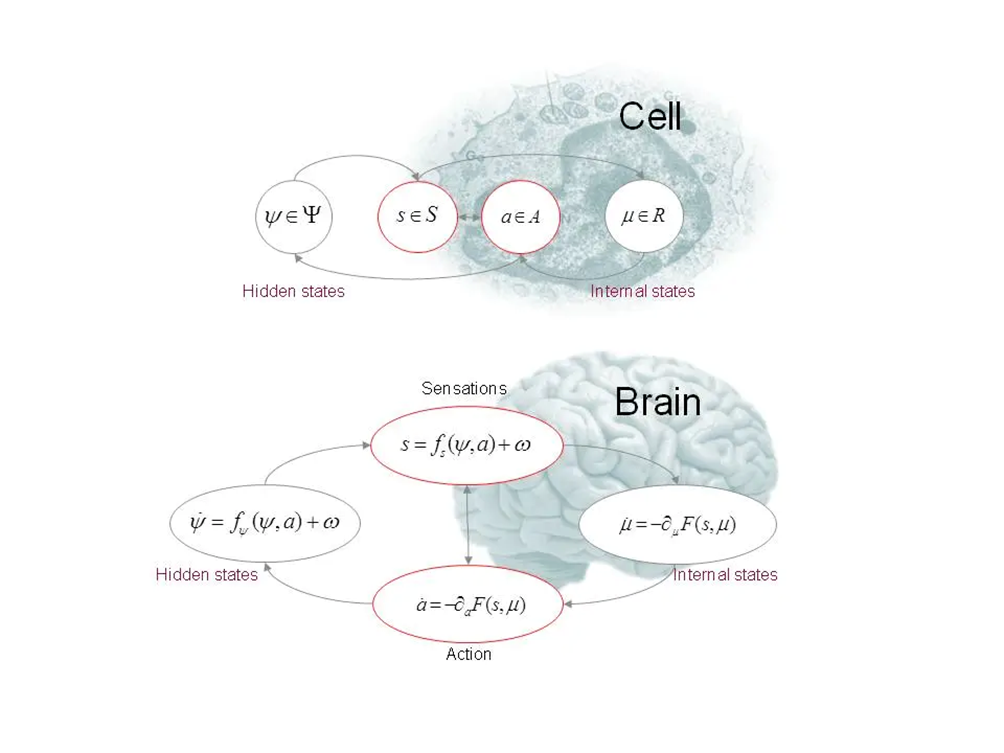
图1. 自由能原理尝试从第一性原理出发为生命和智能提供统一的解释。

1. 生命、意识与智能的统一原理

在探讨生命起源到意识奥秘这一宏大话题时，许多科学家曾做出重要贡献。例如，达尔文在《物种起源》中提出了演化论，认为生物的多样性和复杂性是通过自然选择和适者生存的过程逐渐形成的。薛定谔在《生命是什么》中探讨了生命体如何在物理定律的框架内维持其高度有序的状态，特别是通过引入“负熵”的概念来解释生命体如何抵抗热力学第二定律所描述的无序趋势。他指出，生命系统通过与外界环境交换物质和能量，实现了内部的秩序和复杂性，这与开放系统通过能量流动维持秩序的思想相呼应。

普利高津的耗散结构理论进一步阐释了开放系统如何在远离平衡态的条件下，通过能量和物质的流动生成和维持秩序。这一理论解释了在非平衡状态下，系统如何通过耗散过程形成新的稳定结构，这些结构表现出高度的组织性和复杂性，与生命系统的特征相吻合。普利高津的工作扩展了我们对生命系统如何在动态过程中维持其复杂性的理解，可以视为是对薛定谔“负熵”概念的物理和数学上的深化与扩展。

现在，探索生命及意识起源奥秘的接力棒交到了自由能原理手中，这可能是我们距离揭示生命和意识起源以及智能的奥秘最近的一次尝试。我们发现，这与以预测为核心的大语言模型之间存在许多相似之处，对于下一代人工智能算法的开发，或许能够带来新的的洞见和启示。

自由能原理（Free Energy Principle, FEP），由当前全球最具影响力的理论神经科学家 Karl Friston 提出，它揭示了生物系统如何通过最小化内部状态与外部环境预期之间的差异，即最小化自由能，来实现与环境的和谐共存和维持内部稳态。这一理论在过去二十年间不断深化，其理论基础根植于生物物理学和系统生物学，广泛应用于神经科学、认知科学和心理学领域，并对新一代人工智能算法产生了深远的影响。

图2. 达尔文，薛定谔，普利高津，和Karl Friston 。｜来源于网络

基于自由能原理的主动推理（ActiveInference）提供了一个统一的框架，用于建模感知、学习和决策过程。在这一框架中，感知和行动被视为推断过程的一部分。主动推理进一步阐释了这一过程，它不仅包括被动适应环境，还涉及主动通过行为改变环境，以实现预期状态。

主动推理理论的核心观点是，生物体的认知和行为都遵循相同的规则，即最小化感官观测的惊奇（surprise）。惊奇是衡量智能体当前感官观测与偏好观测之间的差异的指标。

在主动推理框架下，感知过程可以看作是调整智能体脑中的信念，使其与观测尽可能一致。例如，当我们在路上行走，远看一个人影，走近后发现其实是一棵树，我们就更新了之前的错误信念。另一方面，行动过程则是通过改变世界，使感官观测与我们的信念（脑中的先验信念、偏好、表现型）尽可能一致。比如，我们在路上行走时突然遇到大雨，为了避免被雨淋湿（这可以看作是我们脑中的先验信念），我们会迅速寻找避雨的地方，通过行动改变了感官观测，使世界状态与我们的预期相符。

主动推理理论框架可以通过两条路径来理解：一条是更贴近日常直觉的贝叶斯路径（Low road），另一条是更符合底层原理的物理路径（Highroad）[6]。接下来，我将简要介绍这两条道路的思路和逻辑。关于这两条道路的更深入内容，将在后续的文章中进行详细讨论。

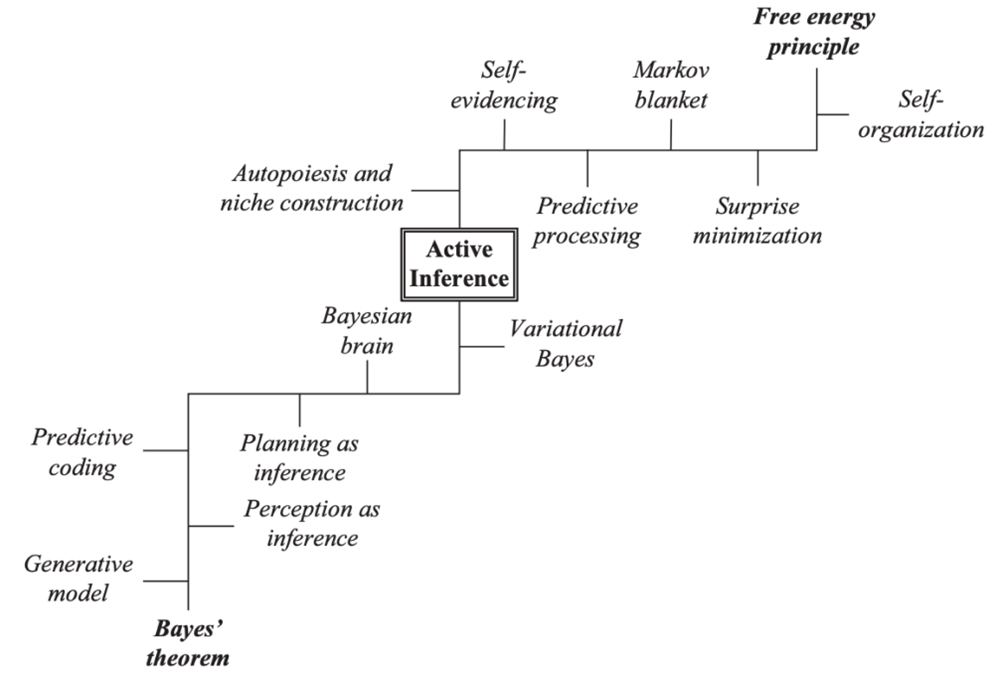
图3. 主动推理的两条路径：贝叶斯路径（Low road）和物理路径（Highroad）

2. 主动推理的第一条道路：从贝叶斯定理出发

在介绍贝叶斯定理的主动推理路径之前，我们首先需要区分一组关键概念：生成过程（Generative Process）与生成模型（Generative Model）。生成过程指的是现实世界中实际发生的事件过程，反应了现实世界的真实状态以及这些状态如何决定我们的观测结果。相对地，生成模型则是智能体（无论是人类还是人工智能系统）对世界的信念和理解的内部表示。

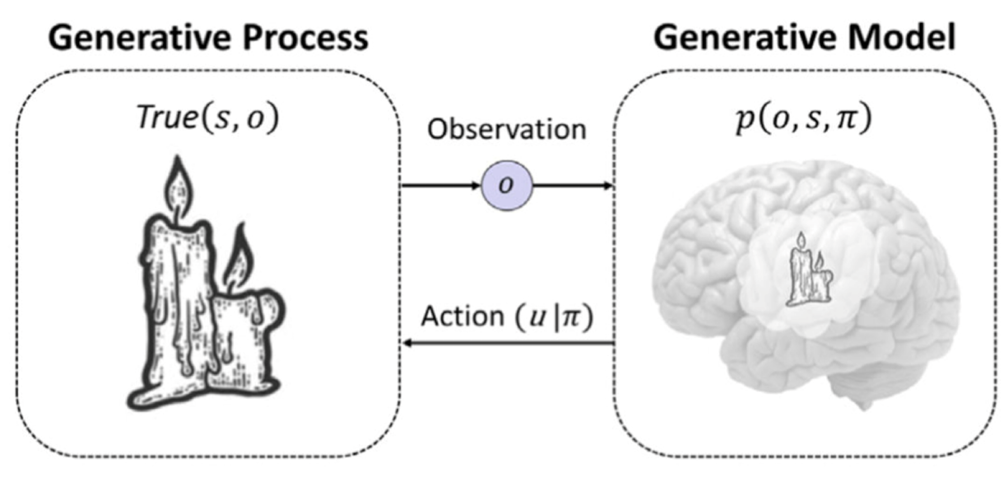
图4. 生成过程和生成模型

由于我们无法直接知晓真实世界的生成过程，只能依据观测到的有限信息来构建对真实世界的认知。智能体通过这些观测信息在其大脑中构建一个模型，力图尽可能地复原外部世界的生成过程。在人工智能领域，这种内部构建的模型有时也被称为“世界模型”。

古希腊哲学家柏拉图提出过一个著名的洞穴思想实验，抛开更深层次的隐喻，这里不太严谨的借用这个实验进行举例：想象一个深洞穴，里面有一群囚徒自出生以来就被锁链束缚，面朝墙壁，不能转身看到背后。在他们背后有一堆火，火光将洞穴外走过的人和手持物体的影子投射到囚徒面前的墙壁上。由于囚徒只能看到这些影子，他们便认为影子是现实世界的全部。其中生成过程对应外面士兵及他手持的三维物体的运动，这是现实世界状态的真实演变。而洞穴中的囚徒所看到的，不过是这些三维物体在墙上的二维投影，这构成了囚徒头脑中的生成模型。囚徒所能做的就是通过阴影来推断物体的真实形态。

图5. 柏拉图洞穴思想实验

这种根据已知观测信息去推断未知信息（在这里指世界背后的真实状态）的过程就是贝叶斯定理的核心思想。例如，当我们从远处辨认一个模糊的轮廓时，我们可以运用贝叶斯定理来评估这个轮廓是人还是树的概率，并据此做出推断，这个过程通常是在我们大脑的潜意识中自动完成的，并不需要进行刻意的、有意识的计算。这种由观察结果反推原因的方法，展示了智能体如何利用已有的信念和新的观测数据不断更新对世界的理解。

例如，我们的视觉感知不仅仅是被动地接收外界的信息，而是包含了一个主动的推断过程。在一些情况下，如果呈现给我们的视觉信息是模糊或误导性的，大脑会根据以往的经验和预期来做出推断，导致我们“看到”一些实际上并不存在的事物。一个例子是著名的“缪勒-莱尔错觉”（Müller-Lyer illusion），两条相同长度的线因为箭头的指向不同，给人造成了长度不同的错觉。

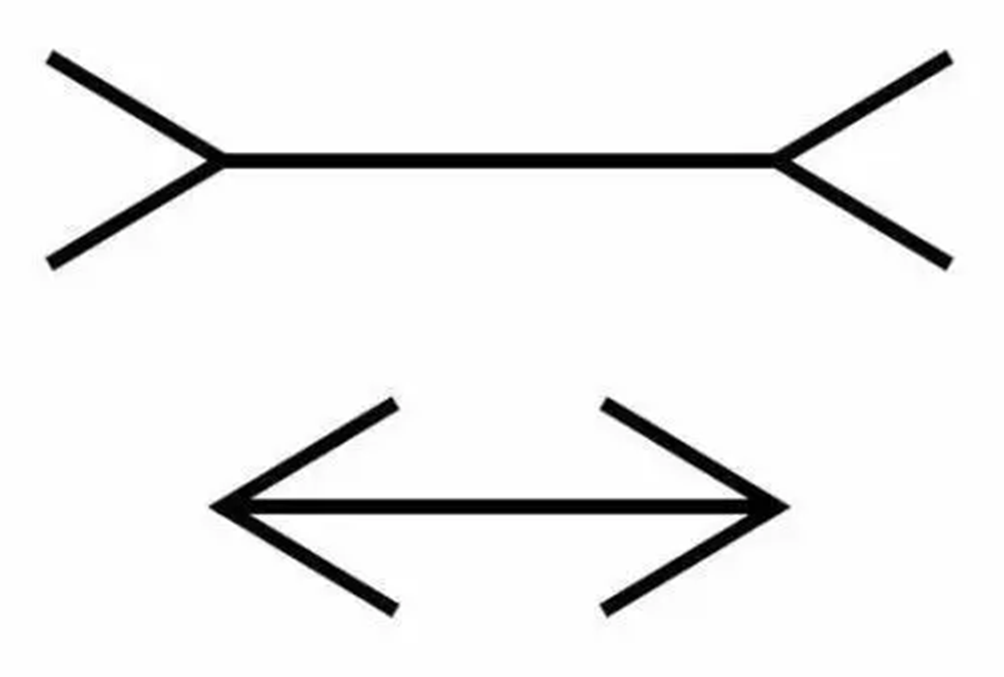
图6. 缪勒-莱尔错觉

19世纪德国物理学家赫尔曼·冯·亥姆霍兹（Hermannvon Helmholtz）是首位将大脑比作一个假设检验机器的科学家。他提出，人类的感知系统可以被视为一个统计推断引擎，功能是根据感官输入来推断最可能的原因。亥姆霍兹对产生知觉的“物理活动”进行了如下描述：“（它们）一般不是有意识的，而是无意识的。就结果来看它们就像推理活动，因为我们是从观察到的感官结果得出这种结果的原因。即使我们实际上只能直接接触神经层面的事件，也就是说，我们感知到的是感官结果，而不是外部对象。”（亥姆霍兹，1867年，翻译来自《预测心智》一书中文版）

到了20世纪末，Peter Dayan和Geoffrey Hinton在他们的开创性工作“sleep-wake算法”和“亥姆霍兹机”中[1,2]，将热力学与统计物理学中的自由能概念引入机器学习领域。在热力学中，亥姆霍兹自由能定义为系统的能量减去其熵与绝对温度的乘积，用公式表示为 F=U-TS，其中U是系统的内能，T是温度，S是熵。在机器学习中引入变分分布后，变分自由能的概念被提出，它可以视为热力学自由能的信息论同构物。变分自由能通过结合模型的生成概率和观测数据的概率分布，为学习算法提供了一个优化目标。在这一框架下，变分自由能的最小化等价于数据的最大似然，这使得学习过程可以看作是在寻找能够最好解释观测数据的模型参数。

进入21世纪，这一关于感知推断的视角得到了进一步的发展，形成了所谓的“贝叶斯大脑假说”，它将大脑的感知和决策过程视为一个贝叶斯推断的过程。这一假说认为，大脑不断地根据先验知识和新的感官证据更新其对世界的估计和预测。

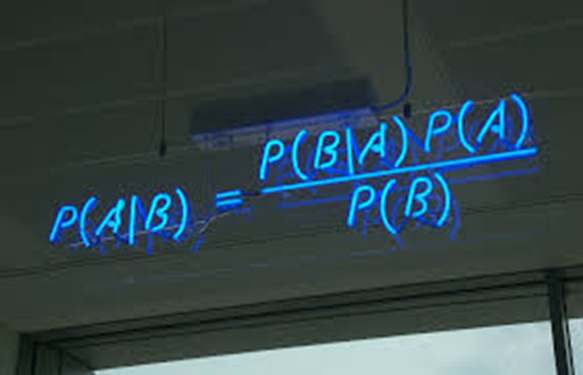
图7. “贝叶斯大脑假说”将大脑的感知和决策过程视为一个贝叶斯推断的过程。

上图是贝叶斯定理的数学形式，贝叶斯定理是概率论中的一条重要定理，告诉我们如何依据观察到的结果逆向推断出潜在原因，可以看作是一种由果溯因的推理方式。以贝叶斯定理为基础，我们可以将智能体的感知和行动过程视为贝叶斯推断的实践。在感知方面，我们根据观测到的状态来推断和更新对世界真实状态的估计；而在行动方面，我们依据自身的偏好和信念来推断应采取的行动。

然而，从公式中可以看到仅凭贝叶斯公式直接获得状态的后验估计面临一个复杂的数学挑战。观测的边际概率P(B)需要对所有可能的状态进行积分才能得到。为应对这一难题，我们引入一个近似的后验分布，将推断问题转化为最优化问题：寻找一个近似后验分布，使其尽可能地接近真实后验分布。变分自由能作为衡量两者距离的上界，我们的目标便转变为最小化这一变分自由能，以此达到优化推断的目的。关于变分贝叶斯更详细的内容以及具体的公式推导会在后续系列文章中进行介绍。

感知、模型学习和动作选择均可以理解为追求最小化自由能的过程。在这一过程中，感知与模型学习主要依托于当前及历史观测数据，而动作选择则着眼于未来还未发生的观测数据。在主动推理的框架下，根据时间维度的划分，自由能被分解为两个部分：一部分是着眼于过去的变分自由能，它涉及对现有和历史数据的分析；另一部分是着眼于未来的期望自由能，它关乎通过行动使得未来的观测数据符合预期信念。

从贝叶斯定理演进到主动推理的道路中，我们看到了什么是自由能，以及如何最小化自由能。然而，一个更深层次的问题尚未得到解答：为何我们会追求最小化自由能，或者说，为何生物体要致力于最小化惊奇（surprise）？为了深入这一问题，我们需要将视野提升至更高层次——透过随机动力系统这一数学物理视角，我们将看到生物体得以存在的必要条件就是最小化自由能。

通过这种高层次的分析，我们开始理解，自由能最小化不仅是一个数学上的概念，而是生物体适应环境、维持内部稳态、并有效预测未来事件的关键机制。这一原理指导着生物体如何通过内部模型来预测和解释外部世界，从而在不断变化的环境中生存和延续。

3. 主动推理的第二条道路：从随机动力系统出发

生物系统可以被视为一个处于非平衡稳态的开放系统，它们不断地与外界交换物质和能量。在数学上，这类系统可以被建模为随机动力系统，以捕捉其内在的动态性和随机性。其中，“非平衡”指的是系统与外界之间有能量或物质的交换，意味着系统不是封闭的，也不是静止的，而是处于持续的变化之中。而“稳态”则指尽管有交换发生，系统的一些宏观性质在一定时间内相对稳定，表现出一种动态的平衡。这种稳定性是通过系统内部的调节机制和反馈循环实现的，使得生物系统能够在面对环境变化时保持功能和结构的连贯性。

一个典型的例子就是人体的体温调节。无论外部环境如何变化，人体的生理机制都能通过调节血管的扩张与收缩、汗腺的分泌以及代谢率等，保持体温在大约37摄氏度的恒定水平。

从随机动力系统出发的自由能原理路径想要回答的一个核心问题就是，生物系统如何抵抗外界环境波动所带来的耗散效应？换句话说，外界环境在不断变化，如果生物系统不能抵抗这种变化维持内部状态的稳定就会死亡。有两种方式可以维持内部状态的稳定，一种方式是改变内部状态降低对环境的“惊奇”，也就是内部状态应该尽可能准确预测外部的环境状态，另一种方式是通过行动改变外界状态使得内部状态维持在预期的范围内。

还是以体温调节为例，设想你穿着短袖衣物站在冰天雪地的户外，短期内，你的身体会通过内在的调节机制来保持体温接近37摄氏度，这是人体的理想内稳态。这一过程涉及到改变身体的内部状态，以适应外部环境的挑战。然而，如果长时间暴露在如此恶劣的低温环境中，即便是最健康的身体也终将无法承受，无法继续维持这一内稳态，最终导致死亡。幸运的是，与单纯的内部调节相比，我们还拥有另一种强大的能力——通过行动来改变环境状态，进而维持体内温度的稳态。例如，我们可以增添衣物，或是寻找一个温暖的地方避寒。这些行动改变了我们所处的环境条件，帮助我们维持了体内温度的稳定。

需要注意的是，这个例子虽然直观，但它简化了实际情况。实际上，身体对内部状态的调节不仅关注于当前时刻的状态，而是着眼于整个随机动力系统的稳态分布。这种稳态分布受到智能体感知过程和行动策略的影响，不同的感知过程或行动策略可能会导致不同的稳态分布。概括来说，生物体通过复杂的内在调节和行为适应，不断寻求在变化的环境中保持稳态。而那些不那么幸运的生物系统，由于不能有效使稳态分布的熵达到最小化，在自然选择的过程中难以存续。

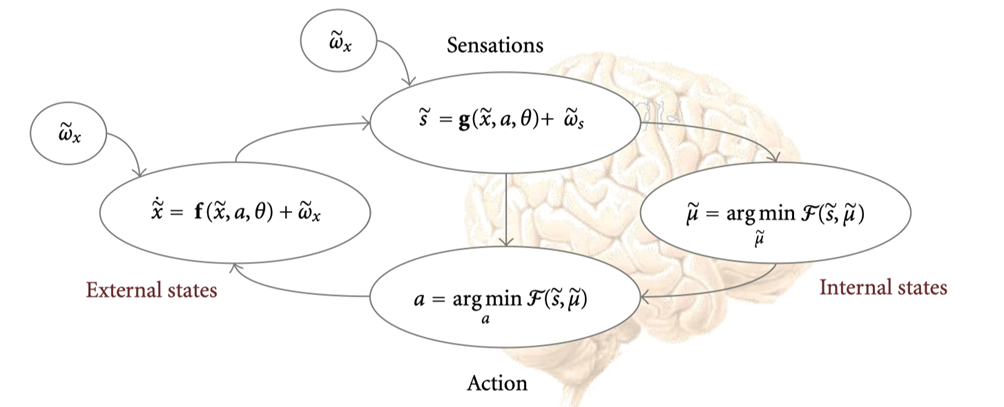
图8. 系统的状态可分为四类：代表外部环境的外部状态（external state）、智能体的观测状态（sensation state）、内部状态（internal state）以及动作状态（action state）。

以上提供了一种直观的理解，从更正式的随机动力系统的角度出发建模生物系统，我们可将系统的状态分为四类：代表外部环境的外部状态、智能体的观测状态、内部状态以及动作状态。在感知过程中，观测状态映射到内部状态，在采取行动策略时，内部状态映射到动作状态。智能体的观测状态和动作状态共同构成了所谓的马尔可夫毯（Markov blanket）。在给定马尔可夫毯的条件下，智能体的内部状态与外部环境状态在统计上是独立的。这种独立性为智能体提供了一种基础，使其能够抵抗环境扰动带来的耗散效应。

正如薛定谔指出，生命系统拥有一种非凡的能力：它们能够抵御外界环境的干扰，违背热力学第二定律所描述的自然趋势，维持自身的有序状态。相较之下，非生命系统往往因无法抵御这些干扰而走向解体。以雪花的消融为例，当它从高空飘落，接近地面时，温度逐渐升高使其融化成雨滴。我们可以说雪花这个物体由于不能抵抗外界温度的升高维持内部状态的稳定从而走向消亡，设想如果雪花能装上一双翅膀，向上飞行，它就能保持原有的形态。

这里，我们所要探讨的问题不仅是生命系统如何能够抵御外界的干扰，更重要的是，一个系统需要满足哪些条件，才能具备这种抵御能力，从而成为我们所理解的生命。答案是只有那些能够最小化自身自由能的系统，才能有效抵抗环境的扰动，持续存在。

图9. 生命系统拥有一种非凡的能力，能够抵御外界环境干扰，维持自身的有序状态，而像雪花这样的非生命系统则不能。

从系统生物学的角度，生命体可以类比为一个处于稳态分布的随机动力系统[4,5]。在这个系统中，我们假设存在可遍历（ergodic）的随机动态吸引子（random dynamical attractor），意味着有一组经常被访问的吸引状态。还是以体温为例，它不会进行无序的随机游走，而是在某个特定值附近波动。该动力系统在长时间演化下，这些吸引状态的时间平均可以代表状态的分布密度，这个密度被称为遍历密度（ergodic density），遍历密度可以通过Fokker-Planck方程的稳态解得到（Fokker-Planck方程表示连续时间随机过程的概率密度函数的演化）。借助于遍历密度的概念，我们得以进一步利用香农熵来定义随机动力系统的遍历熵（ergodic entropy）。遍历熵是对系统长期行为的统计特性的一种度量，它可以被理解为当时间趋向于无穷大时，系统状态的“惊奇”路径积分。在这里，“惊奇”（surprise）指的是状态的负对数似然概率（即-lnp(s)），一个状态的惊奇越大，该状态发生的概率越小。

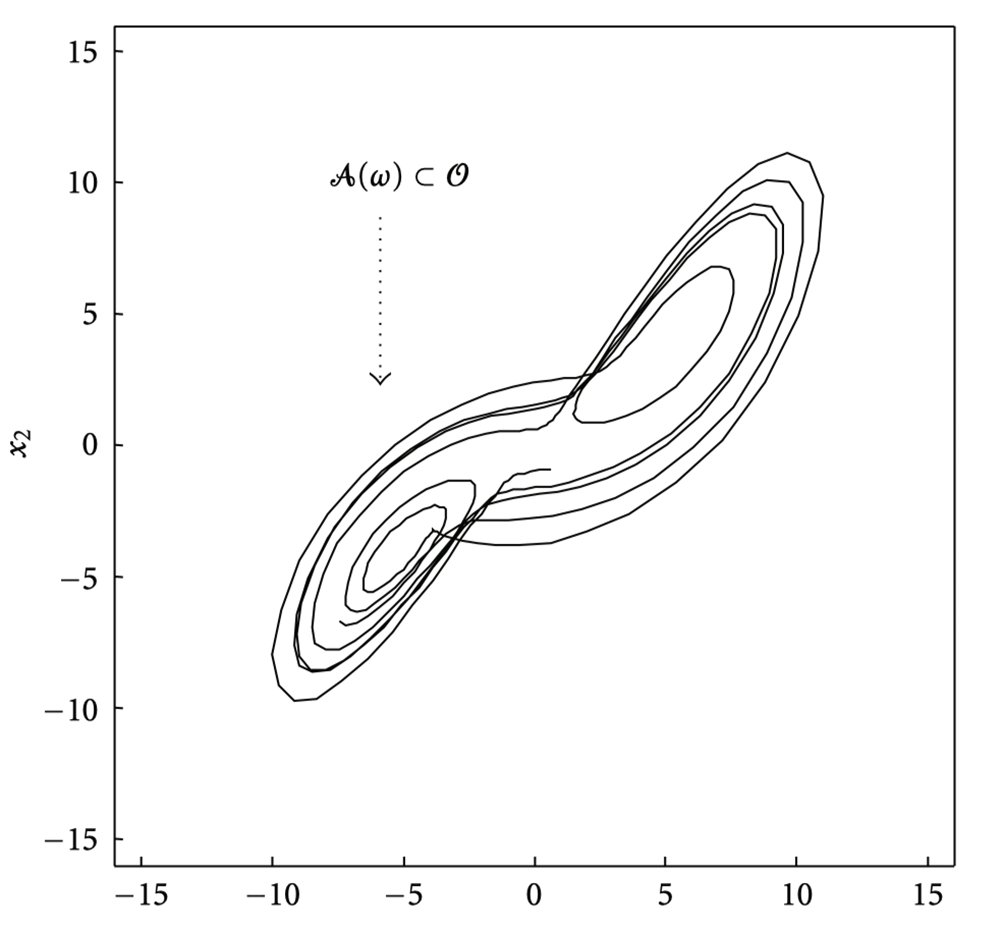
图10. 生命体可以类比为一个处于稳态分布的随机动力系统，我们假设这个系统中存在可遍历的随机动态吸引子。

智能体应该使得系统的遍历熵保持在一个尽可能低的水平。然而，由于智能体无法直接访问外部状态，因此需要通过最小化观测状态的熵，间接地实现对外部隐藏状态熵的控制。为了使观测状态的熵尽可能低，系统需要在内部状态中包含尽可能多的关于外部状态的信息，实现对观测状态尽可能准确的预测，这等同于最小化观测状态的“惊奇”度。换句话说，智能体的感知和动作应该旨在最小化“惊奇”。自由能可以视为感官惊奇的一个上界。因此，通过最小化自由能，智能体实际上也在最小化其“惊奇”。

通过改变感知过程和行动策略，系统能够有效降低自由能，隐含地使得该系统能够将外部状态的“惊奇”最小化，同时使得系统的熵达到最小化，从而维持其有序的存在状态。用一个简单的比喻来说，想象一个在森林中寻找食物的动物。如果这个动物能够预测食物出现的地方（比如通过观察其他动物的行为或者环境的线索），它就可以更有效地找到食物，而不是在森林里随机游荡。通过最小化自由能，动物实际上是在最小化寻找食物时的“惊奇”和不确定性，确保自己能够生存下去。

由此可以看出，最小化自由能是生物系统为了生存和适应环境所演化出的一种必要机制。这一过程将问题从“生物体需要如何行动来获取食物”转变为“为了生存，生物必须执行哪些行动”。可以通过物理学哈密顿力学中局部视角和全局视角进行类比。局部视角关注于粒子在相空间中遵循哈密顿正则方程的具体演化过程。相对地，全局视角——即哈密顿的最小作用量原理——表明，在所有可能的运动路径中，真实的系统演化路径是那条使得作用量取极小值的路径。同样地，智能体采用使自由能取最小值的方式进行感知和行动，这也为什么自由能原理被誉为统一生物体感知和行动的第一性原理。

至此，我们分别从底层路径和顶层路径介绍了自由能原理及主动推理框架的基本思想。作为一种高度抽象的底层原理，自由能原理在认知科学与神经科学领域等具有广泛应用，我们将在下一篇继续介绍。

参考文献

1. HintonG E, Dayan P, Frey B J, et al. The" wake-sleep" algorithm forunsupervised neural networks[J]. Science, 1995, 268(5214): 1158-1161.

2. DayanP, Hinton G E, Neal R M, et al. The helmholtz machine[J]. Neural computation,1995, 7(5): 889-904.

3. FristonK, Kilner J, Harrison L. A free energy principle for the brain[J]. Journal ofphysiology-Paris, 2006, 100(1-3): 70-87.

4. FristonK, Ao P. Free energy, value, and attractors[J]. Computational and mathematicalmethods in medicine, 2012, 2012.

5. KarlF. A free energy principle for biological systems[J]. Entropy, 2012, 14(11):2100-2121.

6. ParrT, Pezzulo G, Friston K J. Active inference: the free energy principle in mind,brain, and behavior[M]. MIT Press, 2022.

7. ClarkA. Surfing uncertainty: Prediction, action, and the embodied mind[M]. OxfordUniversity Press, 2015.

8. Hafner D, Ortega P A, Ba J, et al. Action and perception asdivergence minimization[J]. arXiv preprint arXiv:2009.01791, 2020.

9. Mazzaglia P, Verbelen T, Çatal O, etal. The free energy principle for perception and action: A deep learningperspective[J]. Entropy, 2022, 24(2): 301.

本文为科普中国·创作培育计划扶持作品

作者：牟牧云

审核：张江 北京师范大学系统科学学院教授

出品：中国科协科普部

监制：中国科学技术出版社有限公司、北京中科星河文化传媒有限公司