探索 | 物理学家的伟大贡献（上）

物理探索自然的本质法则，重点在于探讨物质、能量的相互反应和运动规则。借由数学模型与实验观察，物理描绘并理解自然的基本现象，涵盖宇宙至微观粒子的尺度。其终极目标在于揭示宇宙构成的基本原理，构建一个统一的框架来解释所有物理现象。

| 阿基米德阿基米德（Archimedes，公元前287年—公元前212年）作为古希腊的伟大哲学家、数学家、物理学家和力学家，他不仅在静态力学和流体静力学领域奠定了坚实的基础，还以其独特的物理学观点启发了后世无数科学家。

一、力学之父的奠基之作

阿基米德被誉为“力学之父”，这一称号绝非浪得虚名。他首先确立了静力学的基本原理，这些原理为后世的力学研究提供了坚实的理论基础。阿基米德通过深入研究物体的平衡状态，提出了许多至今仍被广泛应用的力学定律和原理。他不仅仅停留在理论层面，更通过实践验证了自己的理论，展现了理论与实验相结合的魅力。

二、浮力定律

解密物体沉浮的秘密阿基米德最为人所熟知的贡献莫过于他的浮力定律，也被称为阿基米德原理。这一原理指出，任何浸入液体中的物体都会受到一个向上的浮力，这个浮力的大小等于物体所排开液体的重量。这一发现不仅解释了为什么船只能够浮在水面上，还为后来的潜水艇技术提供了理论基础。

浮力定律的推导与理解：

为了更直观地理解阿基米德原理，我们可以设想一个简单的实验场景。将一个物体（如木块或铁块）完全浸入水中，我们会发现物体受到一个向上的力，这就是浮力。阿基米德通过精妙的实验和严谨的数学推导，证明了浮力的大小确实等于物体所排开水的重量。这一原理的公式表达为：F浮=G排=ρ液gV排，其中F浮为浮力，G排为排开液体的重量，ρ液为液体的密度，g为重力加速度，V排为排开液体的体积。

三、排水法测量的智慧

阿基米德原理的一个直接推论是排出液体原理。当一个物体浸入液体时，它会排开等于自己体积的液体。这一原理在日常生活和科学实验中有着广泛的应用，特别是在测量不规则物体体积时。我们可以将待测物体完全浸入已知体积的水中，通过测量被排开的水的体积来间接得到物体的体积。这种方法不仅简单易行，而且具有较高的准确性。

四、杠杆原理

平衡与力量的艺术虽然杠杆原理并不直接属于流体静力学范畴，但阿基米德在力学领域的这一贡献同样不容忽视。杠杆原理指出，在杠杆的两端施加不同的力时，杠杆会向力较小的那一端倾斜，但力的大小与力臂（从支点到力的作用线的垂直距离）成反比。这一原理不仅揭示了力与力矩之间的关系，还为后来的机械设计和工程实践提供了重要的理论依据。

杠杆原理的应用：

杠杆原理在日常生活和工程实践中有着广泛的应用。从简单的天平、剪刀到复杂的起重机、吊车等机械设备，都离不开杠杆原理的支撑。阿基米德发明的杠杆滑轮机械更是展现了杠杆原理的巨大威力，他能够利用简单的机械装置牵动满载的大船，这在当时无疑是一项惊人的成就。

| 伽利略

伽利略·伽利雷，16至17世纪意大利人，这位意大利的天文学家、物理学家和工程师，不仅是欧洲近代自然科学的奠基人之一，更是科学方法和科学思维的革命者。他的物理学观点不仅颠覆了当时许多根深蒂固的错误观念，更为后来的科学发展奠定了坚实的基础。

一、自由落体定律

打破重力的束缚在伽利略之前，古希腊哲学家亚里士多德认为，物体的下落速度与其重量成正比，即重物比轻物下落得快。这一观点在当时被普遍接受，并长期束缚着人们的科学思维。然而，伽利略通过一系列精心设计的实验，特别是著名的“两个铁球同时落地”的实验，彻底推翻了这一错误观念。

伽利略在比萨斜塔上进行的实验，用两个重量不同但形状相似的铁球同时释放，结果它们几乎同时落地。这一实验结果直接挑战了亚里士多德的学说，证明了物体的下落速度与其重量无关，而是仅受重力加速度的影响。伽利略进一步提出了自由落体定律：当物体受到重力作用，从静止开始下落的过程，就是自由落体运动，其下落高度与时间平方成正比。这一发现不仅纠正了长期以来的误解，更为后来的经典力学奠定了基础。

二、惯性定律

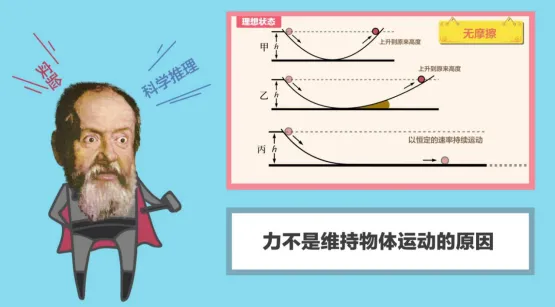
伽利略的另一个重要贡献是提出了惯性定律，也被称为惯性原理或牛顿第一定律的前身。他通过观察物体的运动状态，发现如果没有外力作用，物体将保持静止状态或匀速直线运动状态不变。这一观点与亚里士多德的观点截然相反，后者认为物体需要力来维持其运动状态。

伽利略通过斜面实验，设想了一个理想化的情境：如果斜面足够光滑且无限长，那么物体在斜面上的运动将不会停止，而是会以恒定的速度继续运动下去。这一思想实验虽然无法直接实现，但它却深刻地揭示了物体运动的本质——惯性。伽利略的惯性定律为后来的牛顿力学提供了重要的理论基础，也让我们对运动有了更深刻的理解。

三、相对性原理

伽利略还提出了相对性原理，即在一个惯性系中观察到的所有物理现象，在另一个相对于该惯性系做匀速直线运动的惯性系中观察时，这些物理现象将保持不变。这一原理打破了人们长期以来认为运动是绝对的、静止是相对的错误观念，揭示了运动的相对性。

伽利略的相对性原理对于后来的物理学发展具有重要意义。它不仅为牛顿力学的建立提供了理论支持，也为相对论等现代物理理论的发展奠定了基础。通过伽利略的相对性原理，我们可以更加清晰地认识到，运动并不是孤立存在的，而是与观察者的相对位置和运动状态密切相关的。

四、实验与数学结合的科学方法

伽利略的科学思想方法的核心是把实验和逻辑推理（包括数学演算）和谐地结合起来。他强调科学实验的重要性，认为所有科学结论都应该建立在实验的基础上。同时，他也注重逻辑推理和数学分析在科学研究中的作用，通过精确的数学表达来揭示物理现象的本质和规律。

伽利略的这种科学方法不仅在当时具有开创性意义，也为后来的科学研究提供了重要的方法论指导。他通过实验和数学相结合的方式，成功地揭示了自由落体、惯性、相对性等物理现象的本质和规律，为后来的经典力学和现代物理学的发展奠定了坚实的基础。

五、对天文学和宇宙观的贡献

伽利略在天文学领域也做出了杰出的贡献。他是第一个用望远镜观测天体并取得重要发现的科学家。他通过观测土星光环、太阳黑子、月球山岭、金星和水星的盈亏现象、木星的卫星以及金星的周相等现象，不仅证实了哥白尼的日心说，还推翻了托勒密的地心体系。这些发现不仅极大地扩展了人类对宇宙的认识范围，也为后来的天文学和宇宙学研究提供了宝贵的资料和数据。在当时，伽利略因支持日心说而与罗马天主教会发生冲突，最终在1633年被迫宣布放弃这一观点，并被软禁直至1642年逝世。

| 牛顿

艾萨克·牛顿，17世纪和18世纪之交的英国数学家、物理学家和天文学家，对科学革命做出了巨大贡献。他的物理学观点不仅奠定了经典力学的基石，还深远地影响了科学、工程乃至哲学等多个领域。

一、牛顿三定律

1、牛顿第一定律（惯性定律）

牛顿的第一定律，也被称为惯性定律，是力学中最基础、最直观的定律之一。它告诉我们：“一切物体总保持匀速直线运动状态或静止状态，除非作用在它上面的力迫使它改变这种状态。”这一定律揭示了物体运动状态改变的根源——力。在日常生活中，我们常常能感受到惯性的存在，比如汽车在刹车时乘客会向前倾，这就是因为乘客的惯性试图保持原有的运动状态。

2、牛顿第二定律（运动定律）

如果说第一定律定义了力的必要性，那么第二定律则量化了力与运动之间的关系。牛顿第二定律指出：“物体的加速度正比于作用在它上面的力，反比于它的质量。”即F=ma，其中F是力，m是质量，a是加速度。这一公式简洁而深刻地揭示了物体运动状态变化与外力作用之间的定量关系。它不仅是力学计算的基础，也是理解物体动态行为的关键。

3、牛顿第三定律（作用-反作用定律）

牛顿的第三定律进一步完善了力的概念，指出：“作用在物体A上的力等于物体A对物体B施加的力的大小和方向相反。”这一定律强调了力的相互作用性，即力不会单独存在，它总是涉及到至少两个物体：施力物体和受力物体。同时，作用力和反作用力总是成对出现，大小相等、方向相反。这一观点不仅加深了我们对力的理解，也为后续的动力学分析提供了重要依据。

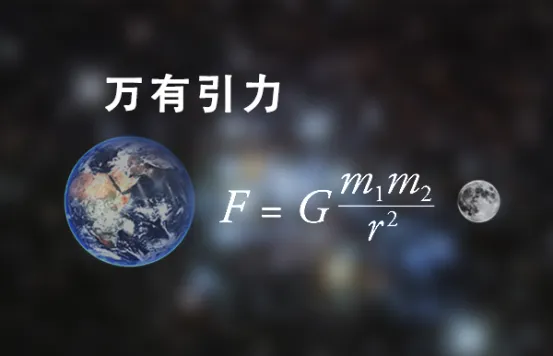
二、万有引力定律

如果说牛顿三定律是描述物体在局部区域内运动规律的基石，那么万有引力定律则是将这一规律推广到整个宇宙的宏伟篇章。牛顿在《自然哲学的数学原理》一书中首次阐述了这一定律：“任何两个物体之间都存在相互吸引的力，这个力与它们质量的乘积成正比，与它们之间距离的平方成反比。”

这一定律不仅解释了地球为何能够围绕太阳运动、月亮为何能够围绕地球旋转等天体力学现象，还为人类探索宇宙、理解宇宙结构提供了重要工具。更重要的是，它打破了古人对天体运动的神秘感，揭示了自然界中普遍存在的引力相互作用规律。

三、光的折射与反射

除了力学和天体力学方面的贡献外，牛顿在光学领域也取得了举世瞩目的成就。他通过精心设计的实验，发现了光的折射和反射规律，揭示了光的波动性质。同时，他还利用三棱镜将白光分解为红、橙、黄、绿、蓝、靛、紫七种颜色的光谱，这一发现为色谱学的发展奠定了基础。

牛顿的光学观点不仅丰富了人类对光的认识，还推动了光学仪器（如望远镜、显微镜）的发展，为后来的科学研究提供了有力支持。更重要的是，他的这些发现挑战了当时流行的光粒子说，为后来的波动说和量子说的兴起奠定了基础。

四、微积分

微积分是研究变化、连续和极限的数学分支，它使得科学家们能够更精确地描述和预测自然界中的各种现象。牛顿利用微积分解决了许多力学和天文学中的复杂问题，如行星运动的轨道计算、物体在重力作用下的运动轨迹预测等。

微积分的发明不仅推动了数学的发展，也极大地促进了物理学、工程学等其他学科的进步。它使得科学家们能够用更加精确和系统的方法来研究自然界中的各种现象，从而推动了人类文明的进步。

（图片源自网络）
作者 | 几维鸟毕业于新西兰林肯大学。对大众科普知识拥有浓厚兴趣，曾在多个科普期刊上发表过科普文章。关注事实，积极探索前沿科技。

初审 | 陈嘉琦复审 | 魏星华
终审 | 周阳