从反函数的观点看逆矩阵

撰文 | 朱慧坚（玉林师范学院数学与统计学院副教授）、丁玖（美国南密西西比大学数学系教授）

我们在之前的文章《矩阵乘法为什么是这样定义的？》中，运用包罗万象的抽象函数概念，论证了矩阵乘法定义中积矩阵元素表达式的合理性和必要性。与矩阵乘积运算直接相关的一个关键术语是“逆矩阵”，同样，我们可以借用反函数的思想来帮助理解这个处处有用的数学对象。

单射和满射

中学教科书里，有一章专讲“反函数”。物理学有个说法，每种基本粒子都有对应的反粒子。可惜，数学不是物理，并非每个函数都有反函数，具有反函数的函数必须满足如下条件：它将定义域一对一地映射到值域上，符合这个要求的函数也被称为单射（injection）。更数学化地说，一对一的函数𝑓: 𝑋 → 𝑌意指，对于定义域𝑋中的任意两个元素𝑥和𝑦，若𝑓(𝑥) = 𝑓(𝑦)，则必定有𝑥 = 𝑦；或言之，一对一的函数将定义域中的不同元素映射成值域中的不同元素。

抽象函数𝑓: 𝑋 → 𝑌定义中的两个集合𝑋和𝑌，第二个集合𝑌可以换成任何一个包含它的集合，在集合论的眼里𝑓没有发生变化，比如一个将定义域𝑋 = {1, 2, … , 365}映射到有理数集𝑌 = 𝑄当中的函数，也可以被视为将同一个定义域映射到实数集𝑌 = 𝑅里；虽然它们各自的𝑌并不相同，但本质上是一样的函数。事实上，任何函数𝑓: 𝑋 → 𝑌中的“目标集合”𝑌都可以换成𝑓的值域𝑅(𝑓)，即所有函数值组成的集合。

这样看来，如果𝑓: 𝑋 → 𝑌是一对一的，那么𝑓: 𝑋 → 𝑅(𝑓)不仅是一对一的，而且是映上的，映上的函数也称为满射（surjection）。同时是单射和满射的函数称为双射（bijection），即对于𝑅(𝑓)中的任意一个元素𝑦，有且仅有𝑋中的一个元素𝑥使得𝑓(𝑥) = 𝑦。我们称双射𝑓为一可逆函数。如果𝑓: 𝑋 → 𝑌将𝑋映射到𝑌之上，给定函数的“映上”条件保证了上述可逆函数定义中的“有”发生，而“一对一”的假设确保了“仅有”成立。本文为了讨论矩阵求逆问题，我们碰到可逆函数𝑓: 𝑋 → 𝑌时总假设它是一个满射，这样，下一段引进的𝑓的反函数将定义在𝑌上。

可逆函数𝑓: 𝑋 → 𝑌意味着𝑋中的所有元素与𝑌中的所有元素，通过𝑓形成了一一对应关系。这种相互对应关系构成了定义𝑓的“反函数”概念之基础。可逆函数𝑓: 𝑋 → 𝑌的反函数是这样定义的：对于𝑌中的任一元素𝑦，被𝑓映射到𝑦的属于𝑋的那个唯一存在的元素𝑥，就是这个反函

算子和可逆矩阵

有了高中生熟知的反函数概念作铺垫，我们可用同样的思想引进大学线性代数中逆矩阵的

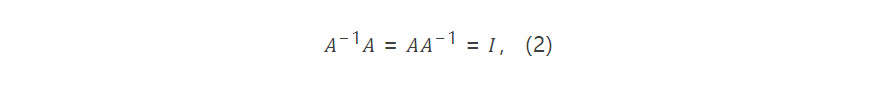
其中𝐼是𝑛阶的单位矩阵，其对角元素为1，其余元素为0。单位矩阵和任何矩阵如能合法相乘，即左边矩阵的列数等于右边矩阵的行数，不论它是左乘还是右乘，结果都是那个被乘矩阵，如同数1在算术中的角色。单位矩阵所对应的线性算子是恒等算子，即它把每个向量映到自己。

在绝大多数线性代数教科书中，公式(2)通常用作逆矩阵的定义，即对于给定的𝑛阶方阵𝐴，如果存在𝑛阶方阵𝐵，使得等式𝐵𝐴 = 𝐼和𝐴𝐵 = 𝐼都成立，则称𝐵为𝐴的逆矩阵。按照如上的算子观点，在此定义中，第一个等式𝐵𝐴 = 𝐼意味着𝐴是一对一的线性算子（因为若非如此，则存在两个不同的向量𝑥和𝑦使得𝐴𝑥 = 𝐴𝑦，从而𝑥 = 𝐵𝐴𝑥 = 𝐵𝐴𝑦 = 𝑦，与𝑥 ≠ 𝑦矛盾）；第二

方阵的“单满等价”

到目前为止，事情似乎进行得很顺利很成功，然而，喜欢思考的读者的脑袋瓜里可能会冒出一个疑问：既然𝐴属于方阵，形状是特殊的正方形，它或许会像方方正正的君子风范一样，具有比一般狭长形或瘦高形矩阵更好的数学品质？具体来说：作为“一对一”线性算子的方阵是否已经自动具备了“映上”的性质？或者对偶性地问：作为“映上”线性算子的方阵是否已经自动具备了“一对一”的性质？如果对于它们的回答都是“Yes, sir”，那么逆矩阵定义中的两个等式就可以只取其中之一，因为另一个就成为直接推论了。

答案确实是肯定的，即对方阵而言，算子性质“一对一”隐含“映上”，反之算子性质“映上”推出“一对一”。为了解释好这两个重要结论，我们假设读者已经知晓线性空间的代数运算，懂得有限维线性空间的维数概念，理解任何矩阵的值域和零空间都是线性子空间，并且至少

结合之前的讨论我们得知，方阵𝐴是单射（满射）当且仅当存在同阶方阵𝐵使得𝐵𝐴 = 𝐼 (𝐴𝐵 = 𝐼)。更进一步，以上的推理论证了只对方阵有效的一个令人喜悦的真理：方阵𝐴如果是一对一的，那么它就是映上的，因此它的逆矩阵存在唯一；方阵𝐴如果是映上的，那么它就是一对一的，因此它的逆矩阵存在唯一。

至此，我们用高中生都学过、但许多大学生都没有真正领会的反函数思想，证明了如下关于逆矩阵的优美定理：

定理 1 设𝐴为一𝑛行𝑛列矩阵，则如下结论成立：

非方阵“最多得其一”

上述用于方阵的定理 1 能推广至非方阵吗？我们先看一个实例，设矩阵𝐴有2行3列。使得𝐴𝐵 = 𝐼的矩阵𝐵必须有3行2列，这时的单位矩阵𝐼为2阶的；满足𝐵𝐴 = 𝐼的矩阵𝐵也必须有3行2列，但此时单位矩阵𝐼为3阶的。我们当前要问的问题是：如果矩阵𝐵满足等式 𝐴𝐵 =

定理 2 的结论在教科书中通常是用“矩阵秩”的性质证明的。矩阵的秩一般用行列式定义：它是矩阵中不等于0的子行列式的最大阶数。秩的性质包括：它不大于矩阵行数和列数之最小值；矩阵积的秩不大于每个因子的秩。在定理 2 中乘积𝐴𝐵和𝐵𝐴的秩都不大于𝑚和𝑛的最小值，而这个最小值小于𝑚和𝑛的最大值，导致结论(i)和(ii)中的等式无法成立。这里采用算子的语言证明了定理 2，避免了对矩阵秩概念的依赖性。

自然，当𝑚 < 𝑛时，一个𝑚行𝑛列矩阵有可能与一个𝑛行𝑚列矩阵相配合，使得它们乘出一个𝑚阶单位矩阵。类似地，当𝑚 > 𝑛时，一个𝑚行𝑛列矩阵有可能与一个𝑛行𝑚列矩阵相配合，

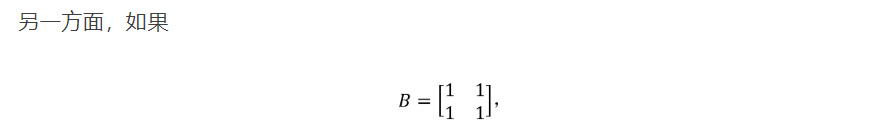
则𝐵将向量(1, −1)映到零向量，故𝐵不是一对一的，因而也不是映上的。

一般矩阵尽管没有经典意义下的逆矩阵，数学家们总有办法在更广泛的意义下定义逆矩阵，称为广义逆矩阵，不过这将是另一篇文章的主题。

怎样求逆矩阵？

没有见过逆矩阵计算公式的读者或许纳闷上例中的2阶逆矩阵是如何获得的。这里我们解析出一般2阶可逆矩阵的逆矩阵公式，并据此推广到一般的可逆矩阵。对于2阶方阵

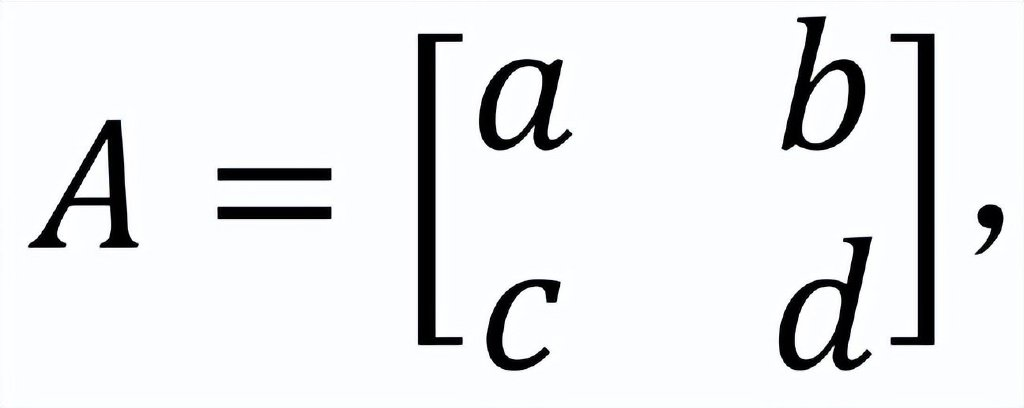
将齐次方程𝐴𝑥 = 0具体写出𝑥两个分量的二元一次方程组

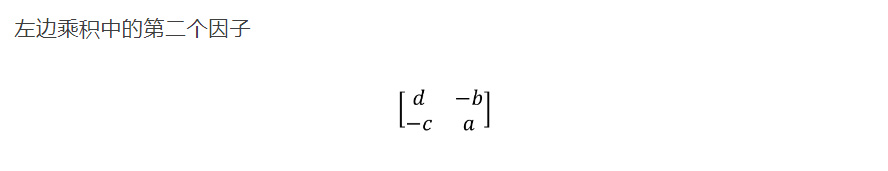
称为原矩阵𝐴的伴随矩阵，记为𝐴∗，但不要理解为常用此记号的𝐴的共轭转置。它的转置矩阵（即第𝑖行第𝑗列元素是原矩阵的第𝑗行第𝑖列元素）的每一个元素可以这样得到：划去矩阵𝐴的对应位置那个元素所在的行和列，剩下一个元素，它同时也被视为该元素所定义的1行1列矩阵行列式的值，再取合适的符号：如果行指标与列指标之和为偶数，则取正号；如果行指标与列指标之和为奇数，则取负号。比如，要算出𝐴∗的第二行第一列元素，划去𝐴的第一行第二列元素𝑏所在的行和列，剩下元素组成的1阶行列式是𝑐，因为1 + 2为奇数，所以在𝑐前添一负号便得𝐴∗的第二行第一列元素−𝑐。

拉普拉斯展开

上面2阶方阵的伴随矩阵概念可以直接推广，但需借用一般行列式的概念。𝑛阶方阵𝐴的行列式|𝐴|在通常的教科书中被定义为𝑛! ≡ 𝑛(𝑛 − 1) ⋯ 2 ∙ 1个带符号乘积之和，其中每个乘积的𝑛个因子取自𝐴中既不同行又不同列的元素，再赋予一个恰当的正号或负号：当这𝑛个元素依

这个行列式的定义语言看似美妙，计算过程却很繁琐，费时费力。好在它有其他等价定义，随时可用，其中一个称为行列式的拉普拉斯展开，由法国数学家拉普拉斯（Pierre- Simon Laplace，1749-1827）首次提出。它的好处是只要定义了𝑛 − 1阶方阵的行列式，就可用这一公式计算𝑛阶方阵的行列式。具体做法是，给定𝑛阶方阵𝐴，任取它的一行或一列，比方说第𝑖行，则

正如此行列式的3!项3个元素乘积代数和定义所得到的结果。

“花瓶”公式

现在可以推导出可求逆矩阵的逆矩阵表达式了。设𝐴为一𝑛阶方阵，它的伴随矩阵𝐴∗被定义

因此，

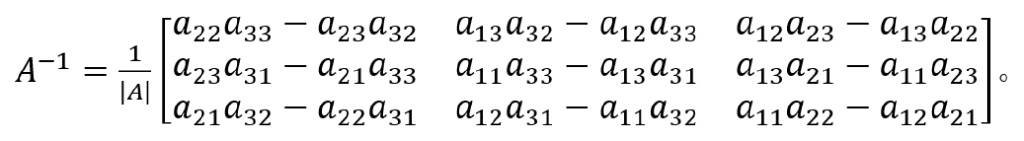
从上面可知，即便对像𝑛 = 3这样很小的可逆矩阵，利用伴随矩阵计算逆矩阵的工作量是可观的，比如当𝑛是不算很大的100时，所需的乘法个数大于100的阶乘，它远远超过10^25，当前最快的计算机也束手无策，跟不上巨量计算的需求。所以，逆矩阵公式(4)只具有理论上的美观性，而缺乏实践上的可行性。

幸亏计算数学家们发展了一套快速计算逆矩阵的算法，其基本思想基于所谓的“高斯消去法”。作为本文的结尾，我们简述用此法求逆的思路。将方阵𝐴和同阶的单位矩阵𝐼放在一排，看成是一个有𝑛行2𝑛列的矩阵，记为[𝐴 | 𝐼]。对该长方形矩阵进行若干初等行变换，只

首先说明，总共有三种初等行变换：(1)交换两行；(2)将一非零数乘上一行；(3)某行乘以一数后加到另一行。这三种“人工操作”都等价于将各自对应的“初等行变换矩阵”乘上被施予变换的原矩阵，而行变换矩阵是对同阶单位矩阵做同样变换的结果。更具体地说，“交换两行”之结果，就是先同法交换单位矩阵的两行，再与原矩阵相乘；“𝜉 ≠ 0乘上一行”等同于𝜉乘上单位矩阵的同一行，再与原矩阵相乘；“𝜉乘上第𝑖行后再加到第𝑗 ≠ 𝑖行”的功效是：对单位矩阵做同样的事，再乘上原矩阵。

需要说明的是，初等行变换不改变可逆矩阵的可逆性，读者可采用本文强调的反函数思想加以证明，方法之一是论证：如果原方阵是一对一的，则每一种行变换后的矩阵也是一对一的。特别地，由于初等行变换矩阵是对可逆的单位矩阵施加行变换的结果，所有行变换矩阵都是可逆的。更一般地，初等行变换保持矩阵的秩不变，但这里我们不再追问“秩”概念的相关推论，留待今后专文谈它。从前面“算子和可逆矩阵”小节中的最后一段可以得出，有限个可逆矩阵的乘积矩阵也是可逆

几何观点

在数学中，任何代数运算都伴随着逆运算的概念，在抽象函数的范畴里，一对一加上映上这两种性质就引出了反函数的术语，将这个高中生早就学过、具有广泛用途的一般概念，用于方阵所定义的将欧几里得空间映到自身的“有限维线性算子”这一特殊情形，我们就可以用反函数的观点看逆矩阵。这种观点，可能比看似简洁的“𝐵𝐴 = 𝐴𝐵 = 𝐼”式逆矩阵定义更具几何特色，因而更为直观，更易于理解，并且“直捣”逆矩阵概念的数学核心。这个观点所体现的教学思想，在匈牙利裔美国数学家哈尔莫斯（Paul Halmos，1916-2006）的名著《有限维线性空间》（Finite-Dimensional Vector Spaces）中处处可见，也在他的徒孙阿克斯勒（Sheldon Axler，1949-）已再版多次、脍炙人口的大学生教科书《线性代数应该这样学》（Linear Algebra Done Right）中继承下来。

阿克斯勒教授走得更远，1995年，他在《美国数学月刊》上发表了一篇阐述性文章《打倒行列式！》（“Down with determinants!”），标题口号也是文章的最后一句，其中的“打倒”一词，会让对它记忆犹新、65岁以上的中国人“大吃一惊”。这篇号召“横扫数学牛鬼蛇神”的战斗檄文，第二年让他将美国数学协会的Lester R. Ford写作奖收入囊中。不过，因为几乎所有线性代数教科书都讲行列式，我们在本文依然用它写下不实用的逆矩阵漂亮公式。我们再次强调，将变换的目光投向逆矩阵的园地，便有几何的阳光照进线性代数的课堂。

特 别 提 示

1. 进入『返朴』微信公众号底部菜单“精品专栏“，可查阅不同主题系列科普文章。

2. 『返朴』提供按月检索文章功能。关注公众号，回复四位数组成的年份+月份，如“1903”，可获取2019年3月的文章索引，以此类推。

版权说明：欢迎个人转发，任何形式的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。