《熵与信息》03：麦克斯韦妖的百年纠葛

熵与信息（三）：麦克斯韦妖的百年纠葛

任何一个上过中学的人都知道热力学第二定律，正因为这条定律，第二类永动机才永远无法实现。

虽然我们现在普遍认为热力学第二定律是这个宇宙里最坚实的规律之一，但是它从很早之前就存在一个隐患，这个隐患持续了 100 多年，直到 1982 年才被一位在 IBM 工作的物理学家本奈特从理论上解决掉，而最终的实验验证还要等到 2012 年才由欧洲科学家做出来。

这个隐患就是被人戏称为物理学 4 大神兽之一的“麦克斯韦妖”，是麦克斯韦在 1871 年提出的一个可能违反热力学第二定律的思想实验。

热力学第二定律的“隐患”麦克斯韦妖

这个思想实验是这样的，假设一个容器被分成 A 和 B 两个隔间，中间有一个可以被一个妖怪控制的小门。这个妖怪能观察每一个分子的运动，并根据分子的速度选择性地让它们通过小门。

这样的话这个妖怪就可以让这个门成为某种特殊的单向门，如果是分子的速度大于平均速度，那么它就只能从 A 到 B 通过小门，反过来则不行；如果是分子的速度小于平均速度，那么它就只能从 B 到 A 通过小门，反过来不行。

持续地这样进行，最后只靠分子的热运动就可以做到 A 隔间里的气体分子都比较慢，B 隔间里的分子速度都比较快。从宏观角度来讲，就是做到了只靠热运动就可以让 A 和 B 里的气体温度出现了温差。如果这样的设备真的可以做出来，那么依靠这样的温差就可以设计出来第二类永动机了。

这里的最大问题，就是麦克斯韦妖是不是可以在理论上存在，也就是说它会不会违反物理规律。不过，在最开始的时候别说做出准确的判断了，就是想对这个问题进一步的分析都做不到。本质上来说，麦克斯韦妖也就是一个可以测量信息、记录信息，然后根据信息实现控制的信息系统。但是当时还没有人能清楚地说明信息和物理世界之间的关系。

到了 20 世纪中期，信息论出现了，信息和物理世界之间的一条重要线索，也就是「熵」被发现了。但是信息和物理世界的关系却仍然朦胧不清。

我们都知道，物理学在描述一个物理系统状态的时候用到的是各种各样的物理量，比如长度、速度、能量。绝大多数的物理量都有自己的量纲，也就是说这些物理量归根溯源都来自于对真实世界的测量。如果信息和物理世界是统一的，那么信息量也应该被视为一种物理量。

但是这件事却并没有那么板上钉钉，一直存在争议。这里主要有 2 个原因：

第一，物理量来自于对当前真实的测量，这种测量是通过比较而来的。信息量呢？虽然也需要测量，但是这个测量来自于对将来可能性的估计。如果说传统的物理量是通过与标准刻度比较而来的（比如“1 米”是光在真空中 1/299792458 秒移动的距离），那么信息量就是通过数数而来的，通过统计可能性的数量来计算概率（比如上一集里玻尔兹曼熵里的 W）。信息量不依赖于一个系统的具体物理构成，只依赖于它的状态，这也是信息量和熵为什么可以有单位，但是没有量纲的原因。

第二，物理状态的改变往往代表着需要对物理系统做功，做功就代表了系统本身的能量状态需要发生改变。信息状态的改变，需要做功吗？这个事情并不显而易见。比如，一个计算机读写信息，如果完全不考虑电阻的等因素带来的热损耗，信息的改变是不是一定需要做功？

比如，一个 1 点朝上和 4 点朝上的骰子，信息状态肯定不同，但是它们的能量状态很难说清楚哪个更大，哪个更小。还比如，一张写了字的纸和空白的纸，哪个能量更大呢？

两个争议点中，第一点还比较容易理解，因为这问题本身取决于信息量和物理量的具体定义，争议的是我们是否要将物理量的定义扩大到可以囊括信息。第二个问题就不一样了，信息和能量的关系不是靠定义就可以改变的，而需要进一步研究才能揭露出其中隐藏的规律。这就需要用到前面提到的线索——熵。

熵和信息的关系，我们在前面几集里面已经介绍过了，香农在创立信息论的时候已经确立了。而熵和能量关系的确立，其实更早，毕竟熵最开始提出来就是为了解决和能量有关的热力学问题。而最早发现熵和能量关系的就是热力学第二定律的奠基人之一、熵这个概念的发明人——克劳修斯。

克劳修斯熵

在克劳修斯之前，人们已经隐隐约约发现热机的效率无法无限提高，但是如何用数学描述这个问题还不清楚。

克劳修斯之前的科学家就注意到了这样一种情况，假如一个物理系统的变化是一个可逆过程，比如理想弹簧的压缩和伸展，相变过程，热平衡状态下 0 摄氏度的水变冰冰变水，能量不应该有变化。

但是绝大多数的非理想情况都不是这样的，比如现实中的弹簧，不论是从伸展到压缩，还是从压缩到伸展都是会有能量损耗。而且，在这个过程中，能量以热量的形式被消耗，因此也称为热损耗。

在物理课本往往都是用一个卡诺机的状态变化图来展示一个类似过程，其中 p 代表气体的压强，V 代表气体体积。

熵与信息（三）：麦克斯韦妖的百年纠葛

任何一个上过中学的人都知道热力学第二定律，正因为这条定律，第二类永动机才永远无法实现。

虽然我们现在普遍认为热力学第二定律是这个宇宙里最坚实的规律之一，但是它从很早之前就存在一个隐患，这个隐患持续了 100 多年，直到 1982 年才被一位在 IBM 工作的物理学家本奈特从理论上解决掉，而最终的实验验证还要等到 2012 年才由欧洲科学家做出来。

这个隐患就是被人戏称为物理学 4 大神兽之一的“麦克斯韦妖”，是麦克斯韦在 1871 年提出的一个可能违反热力学第二定律的思想实验。

热力学第二定律的“隐患”麦克斯韦妖

这个思想实验是这样的，假设一个容器被分成 A 和 B 两个隔间，中间有一个可以被一个妖怪控制的小门。这个妖怪能观察每一个分子的运动，并根据分子的速度选择性地让它们通过小门。

这样的话这个妖怪就可以让这个门成为某种特殊的单向门，如果是分子的速度大于平均速度，那么它就只能从 A 到 B 通过小门，反过来则不行；如果是分子的速度小于平均速度，那么它就只能从 B 到 A 通过小门，反过来不行。

持续地这样进行，最后只靠分子的热运动就可以做到 A 隔间里的气体分子都比较慢，B 隔间里的分子速度都比较快。从宏观角度来讲，就是做到了只靠热运动就可以让 A 和 B 里的气体温度出现了温差。如果这样的设备真的可以做出来，那么依靠这样的温差就可以设计出来第二类永动机了。

这里的最大问题，就是麦克斯韦妖是不是可以在理论上存在，也就是说它会不会违反物理规律。不过，在最开始的时候别说做出准确的判断了，就是想对这个问题进一步的分析都做不到。本质上来说，麦克斯韦妖也就是一个可以测量信息、记录信息，然后根据信息实现控制的信息系统。但是当时还没有人能清楚地说明信息和物理世界之间的关系。

到了 20 世纪中期，信息论出现了，信息和物理世界之间的一条重要线索，也就是「熵」被发现了。但是信息和物理世界的关系却仍然朦胧不清。

我们都知道，物理学在描述一个物理系统状态的时候用到的是各种各样的物理量，比如长度、速度、能量。绝大多数的物理量都有自己的量纲，也就是说这些物理量归根溯源都来自于对真实世界的测量。如果信息和物理世界是统一的，那么信息量也应该被视为一种物理量。

但是这件事却并没有那么板上钉钉，一直存在争议。这里主要有 2 个原因：

第一，物理量来自于对当前真实的测量，这种测量是通过比较而来的。信息量呢？虽然也需要测量，但是这个测量来自于对将来可能性的估计。如果说传统的物理量是通过与标准刻度比较而来的（比如“1 米”是光在真空中 1/299792458 秒移动的距离），那么信息量就是通过数数而来的，通过统计可能性的数量来计算概率（比如上一集里玻尔兹曼熵里的 W）。信息量不依赖于一个系统的具体物理构成，只依赖于它的状态，这也是信息量和熵为什么可以有单位，但是没有量纲的原因。

第二，物理状态的改变往往代表着需要对物理系统做功，做功就代表了系统本身的能量状态需要发生改变。信息状态的改变，需要做功吗？这个事情并不显而易见。比如，一个计算机读写信息，如果完全不考虑电阻的等因素带来的热损耗，信息的改变是不是一定需要做功？

比如，一个 1 点朝上和 4 点朝上的骰子，信息状态肯定不同，但是它们的能量状态很难说清楚哪个更大，哪个更小。还比如，一张写了字的纸和空白的纸，哪个能量更大呢？

两个争议点中，第一点还比较容易理解，因为这问题本身取决于信息量和物理量的具体定义，争议的是我们是否要将物理量的定义扩大到可以囊括信息。第二个问题就不一样了，信息和能量的关系不是靠定义就可以改变的，而需要进一步研究才能揭露出其中隐藏的规律。这就需要用到前面提到的线索——熵。

熵和信息的关系，我们在前面几集里面已经介绍过了，香农在创立信息论的时候已经确立了。而熵和能量关系的确立，其实更早，毕竟熵最开始提出来就是为了解决和能量有关的热力学问题。而最早发现熵和能量关系的就是热力学第二定律的奠基人之一、熵这个概念的发明人——克劳修斯。

克劳修斯熵

在克劳修斯之前，人们已经隐隐约约发现热机的效率无法无限提高，但是如何用数学描述这个问题还不清楚。

克劳修斯之前的科学家就注意到了这样一种情况，假如一个物理系统的变化是一个可逆过程，比如理想弹簧的压缩和伸展，相变过程，热平衡状态下 0 摄氏度的水变冰冰变水，能量不应该有变化。

但是绝大多数的非理想情况都不是这样的，比如现实中的弹簧，不论是从伸展到压缩，还是从压缩到伸展都是会有能量损耗。而且，在这个过程中，能量以热量的形式被消耗，因此也称为热损耗。

在物理课本往往都是用一个卡诺机的状态变化图来展示一个类似过程，其中 p 代表气体的压强，V 代表气体体积。

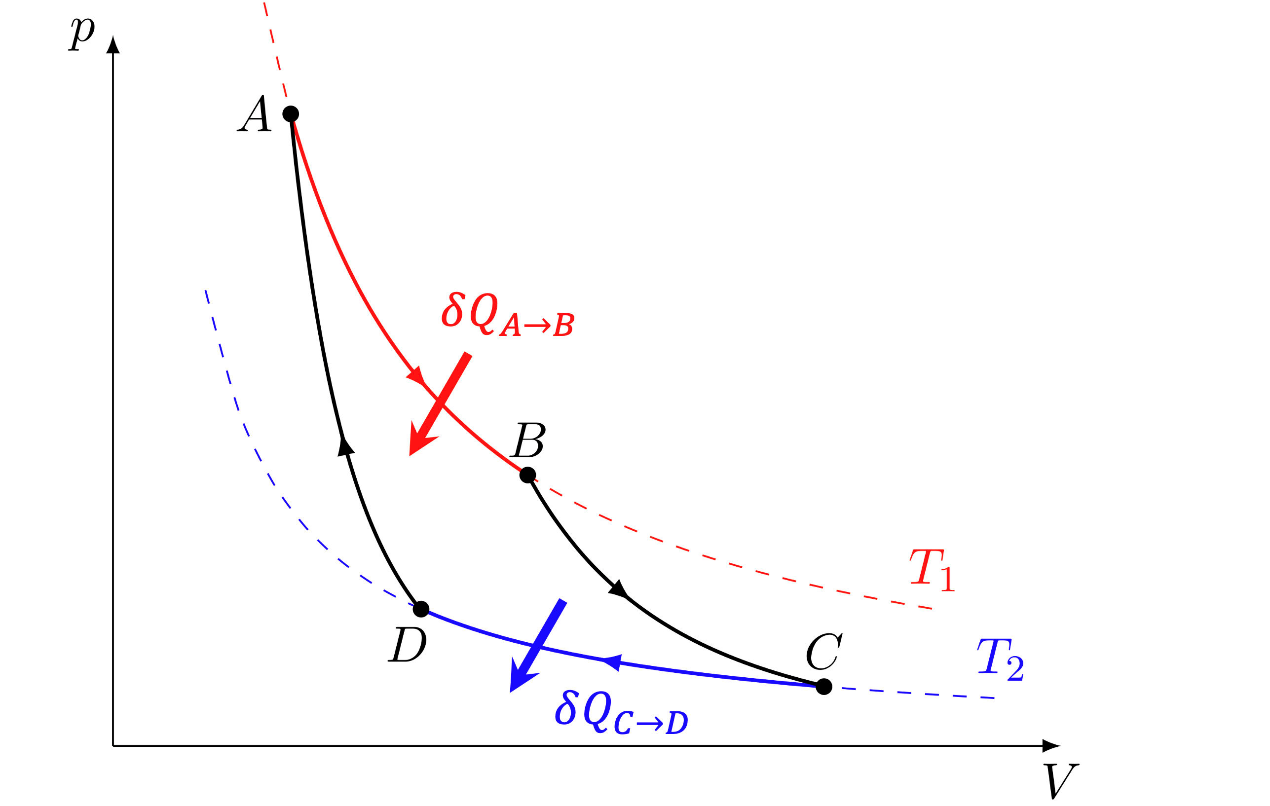
● 过程 A 到 B，是一个等温膨胀过程，温度维持 T1 不变，体积增加，压强减少。这个过程需要吸收热量，吸收的热量为 ，大于0。

● 过程 B 到 C，代表着绝热条件下膨胀，对外界做功，温度下降到 T2 。这个过程虽然温度改变了，也对外做功了，但是因为绝热，所以热量的改变 。

● 过程 C 到 D，是一个等温压缩的过程，温度维持 T2不变，体积减少，压强增大。这个过程需要释放热量 Q2，释放的热量为 ，小于0。

虽然卡诺机一般都是在理想状态下考虑到一个可逆过程，但是对于任何一个状态的循环改变都有下面的关系。

可逆过程：

不可逆过程：

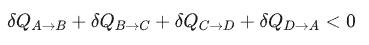
对于不可逆过程，热损耗很容易被注意到，所以上面这样的规律不能说没用，但是会显得比较平庸。而克劳修斯的独创性在于，他发现了系统状态改变时，热量的改变还和温度有关。他发现，在这个过程中的热量变化程度是会和温度成正比的，温度越高需要的热量变化幅度就越大，相反温度越低需要的热量变化幅度就越小。

于是克劳修斯就开创性的把上面的公式给增加上了温度：

可逆过程：

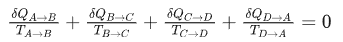
不可逆过程：

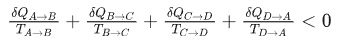
如果状态的改变是连续的，那么这个从一个起点转一圈再回到起点的连续加法，就可以用一个封闭曲线积分表示（也就是沿着图上 ABCDA 一圈连续计算），那么上面还可以统一写成：

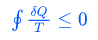
这也就是大名鼎鼎的克劳修斯定理了。值得注意的是，在这个定理中出现了一个全新的物理关系，

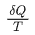
克劳修斯也注意到了这一点，于是就把这样的一个比值定义为了一个全新的物理量——熵（用 S 表示）。也就是：

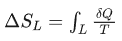
，其中 L 表示任意两个状态之间的路径。

于是前图中的循环过程就可以写作：

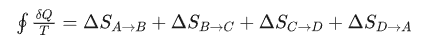
从 A 转一圈回到 A，起点和终点的状态相同，系统的熵必然一样的。对于不可逆的过程，根据克劳修斯定理

计算出来是一个负熵。这个负熵就代表着沿着 ABCDA 的路径变化，如果还想让系统恢复到原先的状态、原先的熵，那么需要对这个系统额外提供

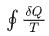
这么多的负熵才行。这个数值越大，代表着 ABCDA 这个路径的热效率越低，会损耗更多能量，也可以说会给环境中带来更多的熵增。

为了把熵这个概念表示的更清楚一些，其实还可以在这个基础上把克劳修斯定理的公式扩展一下，把积分表示换成微分表示，也就是：

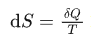
或

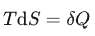
从这里就可以更直观地看到这样一个简单的关系，熵 (S)的改变乘以温度 (T)等于所需要的能量 (Q)。

熵是如何和微观状态产生联系的

克拉修斯提出熵这个概念后自己也没有意识到这件事的价值，因为在当时的人看来，熵这个概念只是一个帮助理解热力学第二定律的辅助概念而已。

虽然克劳修斯对热力学第二定律的表述是，"热量不可能自发地从低温物体传向高温物体"，但是完全可以等价地换成，熵只可能自发地增加，不可能自发地减少。

熵的作用几乎就是一个辅助作用，它甚至都不能被直接测量到，就像是做几何题时画的辅助线一样，有可以更方便，没有也不是不行。

如果一直是这样的话，熵这个概念只会是隐藏在物理学非常角落里的生僻概念。（比如焓就是一个和熵类似性质的热力学概念，但现在绝大多数就都没有听过）

改变这一切的是玻尔兹曼，如果不是他非常天才般地把一个系统的微观状态和熵联系到了一起，让熵成为了一个关联宏观和微观状态的一个桥梁，现在熵也不会成为物理学里最出圈的概念之一。

玻尔兹曼算是克劳修斯的下一代物理学家，克劳修斯 1855 年提出熵的时候，玻尔兹曼只有 11 岁。

在那个年代别说将宏观和微观联系起来了，在当时连物质是不是由分子构成的还被广泛的争论。就比如说当时的著名科学家恩斯特·马赫，他就明确反对分子论。还有，物理化学学科的奠基人，1909 年诺贝尔化学奖获得者奥斯特瓦尔德，也反对分子论。

玻尔兹曼在当时就开创性地思考这样一个问题，如果气体里面全都是一个一个粒子的话，那么当气体的压强、温度、体积等参数处于一个确定状态的时候，其中的粒子都会是如何的？

知道每个粒子的具体状态肯定是不现实的，不过当气体处于平衡状态的时候，还是可以推断出一个粒子在各种不同状态时可能的概率是多少，这个概率值遵循的就是玻尔兹曼分布：

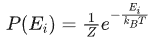
其中：

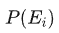● 是粒子处于能量状态 的概率

● Z是配分函数，是所有可能状态的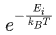之和。即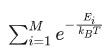， ，M 是所有可能的状态总数。有了配分函数才可以让最后的概率值归一。

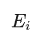● 是粒子在状态 i 时的能量。

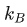● 是玻尔兹曼常数，后面也会直接用k表示。

● T 是绝对温度

具体分布图如下：

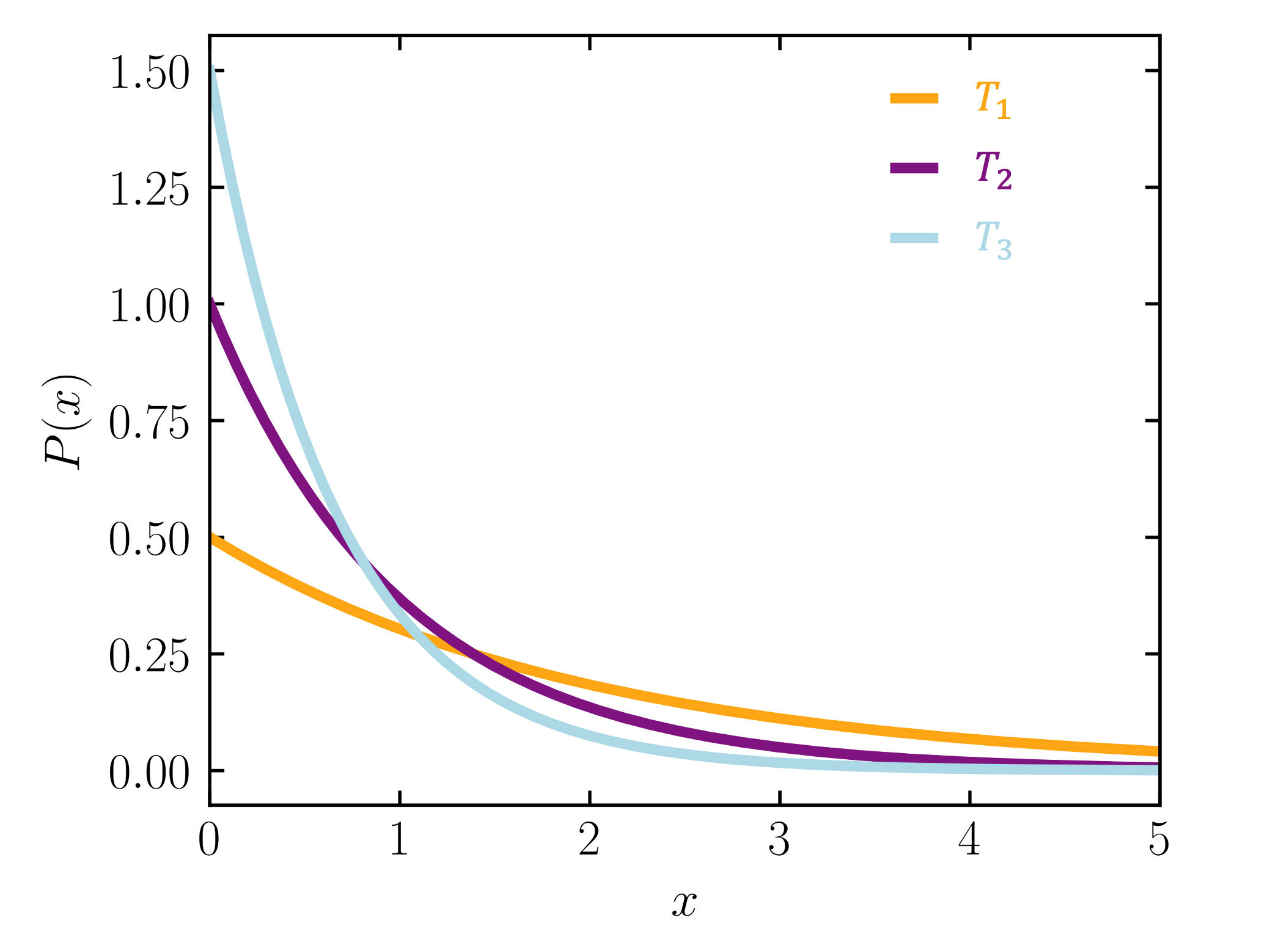
需要注意的是，关于气体粒子的分布图经常见到的还有下面这种。这个其实是麦克斯韦-玻尔兹曼分布的。玻尔兹曼分布和麦克斯韦-玻尔兹曼分布并不一样，玻尔兹曼分布考虑的是粒子的能量状态，麦克斯韦-玻尔兹曼分布考虑的是速度状态。速度和能量之间还相差了粒子的质量，知道粒子质量之后，才可以通过玻尔兹曼分布推导出麦克斯韦-玻尔兹曼分布。这也是为什么下面这个分布图要把气体分子的元素类型标出来，因为元素类型知道了粒子质量也就知道了。

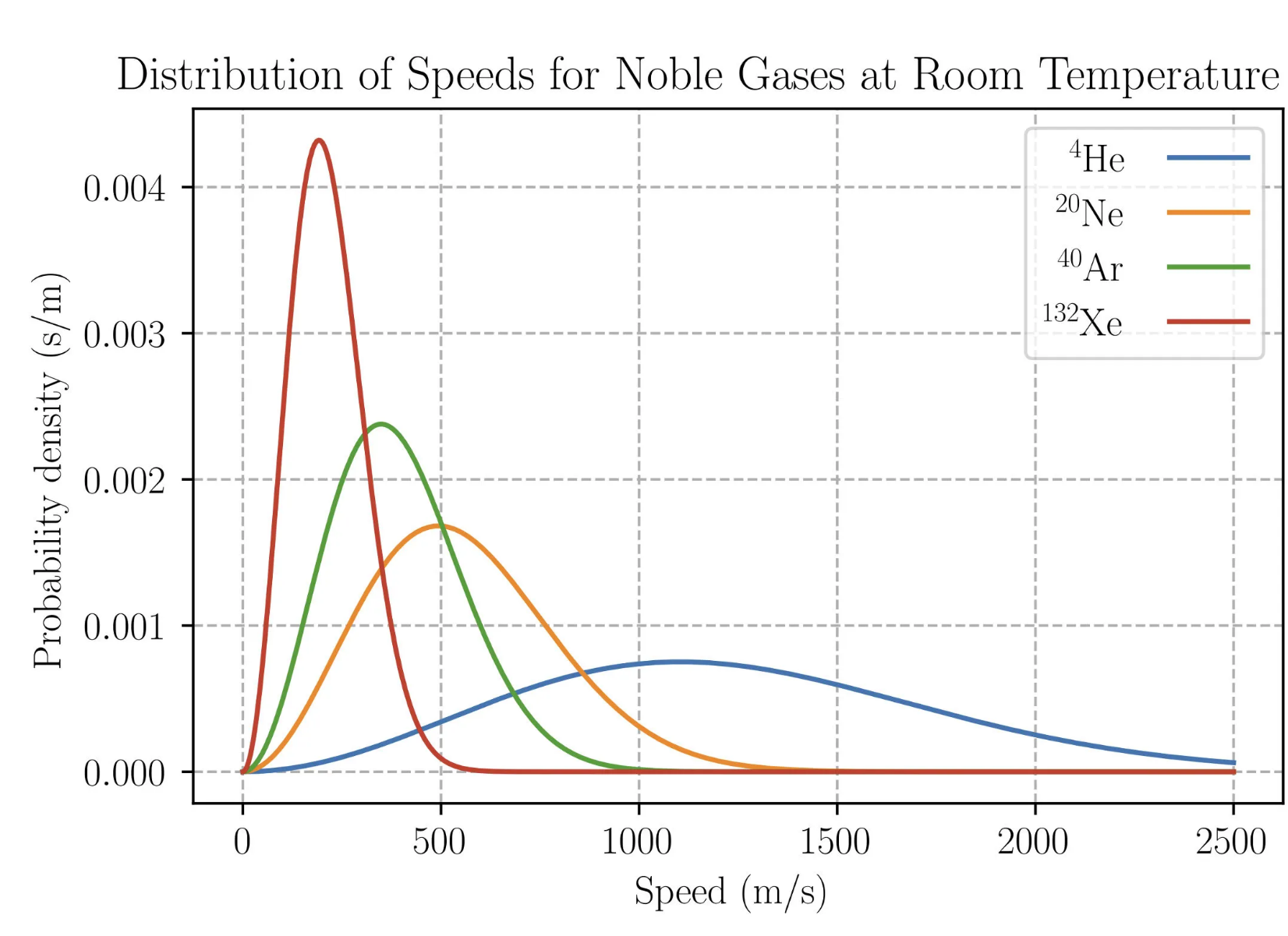
玻尔兹曼推导出分布图之后就发现，一个系统从一种分布曲线切换到另一种分布曲线，一定对应着克劳修斯熵的改变，而分布曲线上每一种可能性的概率值有都和一个粒子的在微观状态上的可能性数量有关。

于是玻尔兹曼就更进一步，用自己扎实的概率论的基础从数学上推导出了克劳修斯熵的微观定义，也就是我们之前介绍过的玻尔兹曼熵：

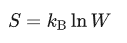
至此熵就成为了一个可以关联微观和宏观状态的关键概念。

兰道尔界限：擦除 1bit 的信息至少消耗多少能量

现在有了两个公式：

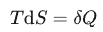
和

通过这两个公式，很容易就可以得到微观状态和能量之间的关系。一个系统从 A 状态变到了 B 状态，其中熵的变化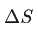是：

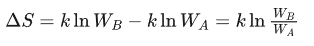
这个过程中系统的热量变化则是如下：（其中正数代表着向环境中吸收能量，负数代表向环境中释放能量）

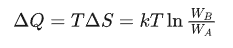
我们最开始考虑的问题其实就是一个系统如果用来记录信息，是不是可以不需要能量也能做到。一个系统想要记录一个信息，其实就代表着这个系统的熵一定发生了改变，也就是上面的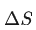不为0。所以现在我们可以确定了，即便是一个单纯的信息系统也无法完全脱离能量。

接下来，就可以更进一步考虑这样一个问题了，如果一个系统想要擦除 1 bit 的信息，最少需要消耗多少能量，也就是需要向环境至少释放多少热量。

这个问题可并不简单，不是简单的让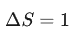就行了，这里有两个原因。

第一，信息量定义里进行 log 运算用到的底是2，而玻尔兹曼熵用到的底是自然常数 e ，这个需要转换。

第二，上一集介绍过信息熵计算的是系统中信息量的平均值，玻尔兹曼熵计算的是一个总值。这其实也很好理解，比如用一份水的温度来表示信息，温暖是 10 摄氏度的时候代表 0，温度是 20 摄氏度的时候代表 1，不论这份水是 1 毫升还是 1 升，温度状态的改变就是 1 bit 的信息改变。但是如果考虑的是玻尔兹曼熵，10 摄氏度的温度变化，1 毫升还是 1 升所要用到的热量可就差别大了。1 毫升只需要很少的热量，1 升却需要很多。所以 1 毫升情况下的玻尔兹曼熵改变的也就更少，毕竟 1 升的粒子数量比 1 毫升多多了，公式里的 W 也要大得多。

所以对于 1bit 信息熵的改变到底需要多少能量，我们只能考虑一个最小值。什么情况下能量最小，当然是系统里面只有 1 个粒子的时候。这样 1bit 信息就代表着，原来粒子可以有 2 种状态，最后变成了只有 1 种状态的情况。也就是：

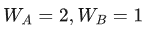
所以有：

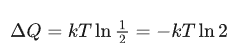
这里的负号代表着是系统需要向外释放能量，所以擦除 1bit 最少需要的能量也就是，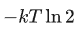

在 20 摄氏度下这个数值大概是 0.0175 eV。

这个最小值现在被称作兰道尔界限，是兰道尔在 1960 年前后提出的。兰道尔在当时不只是提出了这个界限的具体数字，他还在研究中强调了并不是所有的信息处理过程都会有能量消耗，比如“读”、“写”和“复制”数据，它们本质上只是把一种确定的状态变成了另一种确定的状态，系统的可能性本身并没有改变，所以原则上这些操作可以不消耗任何能量。

只有像是信息擦除过程，才有一个能量耗散的下限。这是因为，信息擦除可以认为是这样一个过程：不论之前的状态是 0 还是 1，都统一变成了 0。这就不是将一种确定状态传递变成另一种确定状态了。

所以只有这种情况，也就是只有擦除信息才会消耗能量，而且消耗的能量还有一个下限。现在这个理论也被称为兰道尔原理。

其实在更早的 1951 年，著名物理学布里渊还声称，他发现了一个重要的物理定律：每次测量过程都伴随着一个熵增，而且存在一个熵增下限，如果低于这个下限，测量无法完成。因为布里渊的这个说法当时很多科学家都认为麦克斯韦妖的问题已经解决了。

现在我们知道了，当时布里渊的说法是错的，测量本身并不会改变物体的熵，只有当信息被擦除的时候才会涉及到熵的改变。

在 2011 年，还有科学家进一步研究，他们提出兰道尔认为的擦除信息会导致熵增这一点本身并没有问题，但是熵增并不一定必须体现在能量上。导致熵增的代价可以是别的守恒量，比如角动量的损耗。

关于兰道尔原理，最关键的实验是 2012 年，由美国马里兰大学雅津斯基教授等科学家做出的。他们创造出另一种非常独特的装置，这个装置可以自发地吸收热涨落，把热能转化成机械能。如果只是考虑热力学熵的话，这个装置是违反了热力学第二定律的。因为这个装置不需要额外做功，就可以让热量变成机械能。

不过，这个装置虽然不需要额外做功，但是它却需要持续地消耗空白的存储单元，如果把这部分存储单元所消耗的信息熵也考虑进去，那么这个系统仍然是符合热力学第二定律的。

自发熵减也不会违反热力学第二定律

通过前面介绍可以知道，能将能量和信息联系起来的关键，就是玻尔兹曼对熵给出的微观定义，至此宏观的状态和微观的状态被关联了起来。

这样的关联，虽然可以为我们认识各种物理规律开辟了新的角度（比如兰道尔原理），但同时也为我们理解热二定律带来了新的困难。

比如，就有这样一个让人困扰的问题，从宏观视角下（也就是克劳修斯定理的角度），可以知道一个物理系统是没有办法自发熵减的，要么维持不变要么自发增加。这也是为什么很多人把热力学第二定律称为熵增定律的原因。

但是如果从微观的角度去看，熵增就不一定是必然的了。比如，有两份温度不同的气体放在一起充分混合，这是一个从低熵到高熵到熵增过程，但即便是充分混合后的气体分子，仍然存在着一种可能，在分子随机运动的过程中，恰好高速率的分子全部跑到右边，低速率分子全跑到左边，变成右边的温度高，左边的温度低。也就是说，熵会自发减少的可能性不能绝对排除掉。

这样的话，是不是就否掉了热力学第二定律了呢？还真不是这样。很多人认为的热力学第二定律就是指一个物理系统没有办法自发的熵减，只能不变或熵增，这样理解虽然简单，但是并不严谨。

热力学第二定律严谨的表述有很多，其中比较有名的有三个，分别是克劳修斯、开尔文和康斯坦丁·卡拉泰奥多里，其中卡拉泰奥多里对于大众来说比较陌生，不过在科学界他很有名，他是最先对热力学做出公理化的科学家。

● 克劳修斯表述：

“不可能把热量从低温物体传递到高温物体而不产生其他影响。”

● 开尔文表述：

“不可能制造一种永动机，使其在一个热源上吸收热量并将其全部转化为功而不产生其他影响。”

● 康斯坦丁·卡拉泰奥多里表述：

“在一个系统的任意给定平衡态附近，总有这样的态存在：从给定的态出发，不可能经过绝热过程得到。”

这 3 个表述不用全部理解，只需要知道它们都等价，重点是这里面没有一个提到熵。

当然，你可能说我这是咬文嚼字，通过表述字眼得出结论，是不是太随意了？其实还真不是。如果热力学第二定律真的可以用熵就可以又简洁又严谨的表述出来，科学家们为什么不用呢？毕竟奥卡姆剃刀原则是科学领域里的最基础原则之一。

我们应该明白，热力学第二定律不论用什么样的表述都是外在的形式，它的本质其实在说第二类永动机不能做出来。而我们前面提到的，因为无法排除热振荡而导致出现的自发熵减的情况，并不会否定这一点。

也就是说，即便有偶然的自发性熵减的情况存在，也没有办法实现永动机。

首先，那种自发的熵减情况，即便是真的出现了，因为发生的概率非常小，只可能是零星地会出现，所以不可能持续的发生，也就是它即便是可以对外做功也没有办法持续，没有办法持续当然就不是永动机了。

那是不是可以加一个单向阀门，只保留会带来熵减的热震荡，将那些会引起熵增的情况排除掉？如果可以的话，的确可以持续做功了，但这样，就又变成了一个麦克斯韦妖。我们前面已经介绍过了，麦克斯韦妖是无法实现的。

其实，如果单纯从数学上去看，前面提到的各种表述都默认了一个前提，那就是对应的系统一定是由大规模粒子构成。就拿克劳修斯定理的那个公式来说，里面是用到了微积分的。而微积分这个数学工具如果想有效，那还是有门槛的，它分析的问题需要遵守一个前提，那就是分析的对象（也就是对应的函数图像）需要连续且光滑地变化，只有这样的情况才是可微的。

而如果一个系统里的粒子数量不多，那它的熵的改变就会像是随机过程一样抖动，而随机过程往往都是属于连续不可微的情况（比如布朗运动），无法直接使用微积分进行分析。所以，当我们承认克劳修斯定理是正确的时候，就已经默认了一个系统的熵一定是在连续且光滑地变化，而这只有在粒子规模非常巨大的时候才成立。其他几个表述也类似。

驱动熵发生改变的2个因素

在物理学里有一个概念——状态函数，专门用来指那些仅仅依赖系统初态和终态的的宏观物理量，这些物理量的特点就是只和系统的当前状态有关，与系统如何达到这些状态的过程无关。

我们最熟悉的一个状态函数就是系统的能量状态。比如，许多小球从高处滚落到谷底，不论它从那个方向、以什么样的形式滚落，只要都是在同一个谷底那么它们的势能都是相同的。

熵在这一点和能量非常像，熵也是状态函数，一个系统的熵只和这个系统所具有的状态有关。而且熵和能量还有一个非常重要的相似之处，那就是能量和功是一对，熵和信息量是一对，功是能量状态改变的原因，信息量也是熵改变的原因，功的量纲和能量的量纲相同，信息量虽然没有量纲，但是信息量的单位也可以和熵一样，比如都可以是 bit 。

虽然能量和熵很多地方都很相似，但是在“能量-功”这对组合上很多有用的经验，并不能直接照搬到“熵-信息”这对组合上。

其中第一点，信息量和功的作用是相反的。对一个系统做功，系统的能量是增加的，而对一个系统传递信息，信息是一种负熵，所以系统的熵会减少。当然，这一点区别并不算大，一个是给总量“添油加料”的，一个是给总量“釜底抽薪”的，数学计算上只是一个正负号的差别。

不过在另一个能量和熵的差别上才是最关键的。

能量和功是一个非常简单的因果关系，只要有做功，那么能量一定改变。反过来，只要有能量改变也都有做功。即便是热传递，宏观上虽然不一定会导致做功，但是从微观角度去看，也都是由各种做功活动导致的。

比如，我们通常理解的热传递有 3 种情况，热传导、热辐射和热对流。热传导是微观粒子自己互相碰撞导致的，热传导是微观粒子和辐射光子之间碰撞吸收导致的，热对流就是微观粒子的流动，这些行为本质上都可以看作是做功。

也正是“能量-功”这对组合有这样一个明确的因果关系，所以才会有能量守恒。因为在庞大的物理世界中，不论关系如何复杂，系统之间的能量变化的因果链条都是唯一且等量的。

可如果是熵和信息这一对组合呢？信息的确是熵改变的原因，但却不是熵唯一改变的原因，因为即便是一个封闭系统，即便没有和外界有任何的信息交换，它的熵也是会逐渐增加直到系统达到平衡。

能量之所以能守恒，就是因为它简单明确的因果链条，现在我们知道，熵不具备这个条件，所以熵是不守恒的，宇宙的熵一直在增加。

这里值得多讲一下霍金提到的信息守恒。霍金因为信息守恒才发现了黑洞辐射。前面我们提到过，熵和信息某种程度是一种东西，甚至可以认为信息熵就是一个系统里包含了多少信息量的平均值。如果宇宙的熵不守恒，那是不是信息也不守恒呢？这不和霍金的说法矛盾了吗？

其实并没有矛盾。我们前面提到的熵增的规律，一定是大规模微观粒子里才有的，如果系统里的粒子数量很少，那么熵就会出现在一会儿增一会儿减的震荡，根本没有规律。如果更进一步只考了一个粒子的孤立系统，那它状态将是永恒不变的，当然也就不会涉及到熵的变化了，这个时候熵当然就是守恒的了。

其实，霍金所说的信息守恒里的信息是量子信息，这是把经典信息、经典熵的概念扩展到了量子系统里。不论是经典还是量子，信息和熵的定义都依赖于概率的，经典系统里之所以会有概率存在，是对大规模粒子数量的统计的结果，在这种情况下是由统计规律所支配的（比如大数定律和中心极限定理等）。而单个量子也是有概率存在的，只不过这个概率是由薛定谔方程决定的，而薛定谔方程所决定的概率并不会自发的发生改变。

也就是说，经典的熵之所以会自发地发生改变、无法遵循守恒定律，追根究底还是因为被统计规律所支配，而一个系统可以达到平衡、不再继续熵增，也是因为它在统计规律下系统维持了稳定。

所以，当统计规律不在起效时，比如单个粒子或量子，因果关系有变成单一且确定的了，当然守恒定律就会再次起效。

了解了这些，我们再回头去看克劳修斯定理就会发现其中的巧妙之处，为什么这个定理一定要用闭曲线积分，也就是只考虑那种起点和终点相同的情况去描述。

这是因为只有这样才能排除因为“获取信息”而导致的熵的改变，剩下的一定是在这个过程中因为“统计规律”而导致的改变了。克劳修斯定理的伟大之处就在于，它明确了，要想完全抵消这种改变只能是负值，它的方向是确定的。

因果和相关

驱动熵发生改变有两个因素，一个是信息-熵这样的因果关系，另一个则是统计规律。而就是这个统计规律为我们认知这个世界带来了巨大的挑战，这也是为什么关于热力学第二定律的争论和错误理解有很多。其实“统计规律”对认知带来的挑战并不只是体现在物理学上，在其他各个领域都带来了巨大的挑战。

这是因为我们人都非常习惯利用因果关系进行思考，但是我们又非常不善于发现因果关系。

如果没有专门思考过什么是因果关系这样的问题，那么就会很容易把“ A 发生了之后 B 也发生了”认定为 AB 是一个因果关系，A 是因、B 是果。

对一个系统做功，系统的能量状态发生改变，做功是因，能量状态改变是果。这一点就没有问题。

但如果仅仅这样思考的话，对于熵就会带来巨大的认知挑战，因为统计规律可以自发发生。所以完全可能会有这样的情况出现：

三个人甲、乙、丙，他们的视角不同，甲看到的是 A 发生了之后系统状态发生了改变；乙是看到的 B 发生了后系统状态发生了改变；丙看到的则是 C 发生了后系统状态发生了改变。因为统计规律导致的改变完全是自发的，所以上面 3 种情况完全可以同时存在。这样的话，那么甲乙丙就会得出 3 个不一样的因果关系。

那么如何才能认定一个因果关系呢？其实这个问题现在在科学界中也没有一个定论。不过，值得关注的是图灵奖获得者朱迪亚·珀尔（Judea Pearl）的观点。他之所以获奖，就是因为他在因果关系方面的研究促进了人工智能的发展。

珀尔认为，确定一个因果关系需要有 3 层，也就是他所称的“因果关系之梯”：

● 第一层是“关联”，简单的说就是我们前面提到的 A 发生之后 B 也发生，A B 就是一种关联关系，也可以成为相关。

● 第二层是“干预”，确定一个因果关系不止于被动的观察，还对变量进行主动干预，然后去看干预之后产生的影响。

● 第三层是“反事实推理”，反事实推理是最高层次的因果推理，需要考虑对假设情境的思考。不只要看 A 发生了之后 B 是否发生，还需要考虑如果 A 没有发生，B 是否还会发生。

简单的说，就是如果 AB 是这样一种关系：A 发生了 B 也发生了，A 没发生 B 也一定不发生。那么我们才能将 AB 称作是因果关系。

那么统计规律如果也看作是系统变化的一个原因的话，那么它的反事实推理应该是，如果没有统计规律，是否系统一定不会发生改变。而没有统计规律这件事，别说做干预实验了，就是单纯假设一个不存在统计规律的环境都很困难。

为什么熵会这么晦涩难懂，就是因为“熵变=信息+统计规律”，而和这个公式非常像的还有一个公式“成功=天赋+运气”，统计规律至少还是有规律的，运气那可就是纯纯的随机了。这或许也是为什么关于成功学的书很多，但是书的作者也没有办法把书中的成功复现一遍的原因吧。