阿西莫夫：宇宙的奥秘

【译者之言：从悖论开始，讲述收敛数列和发散数列，从而引出分形理论，继而将其用来解释宇宙的复杂性——“我相信宇宙本质上具有非常复杂的分形特性，对科学的追求也有着共同的特性。这样，宇宙中任何未被了解的部分，和科学研究中任何尚未被解决的部分，与已被了解和已被解决的部分相比，无论多小，它们都包含着原始的复杂性。因此，我们永远都无法将其穷尽。无论我们走多远，前方的路还是会和开始的一样长，这就是宇宙的奥秘。”】

悖论，从自相矛盾的陈述的意义上来说，总是会刺激到我。 我坚定的信念是，宇宙万物的运行方式，都绝不会允许自相矛盾的事情发生。那么，如果我们可能遇到的一些悖论，也只可能是因为我们固执地坚持说一些我们不该说的话。

例如，这里有一个悖论的例子。假设某个小镇上只有一位理发师，他为小镇上的每个人理发，除了那些自己为自己理发的人。问题来了：谁为理发师理发呢？

理发师不能为自己理发，因为他只为那些不为自己理发的人理发。另一方面，如果他不为自己理发，他又会受到“他只为那些不为自己理发的人理发”的说法的束缚。

只有在我们坚持制造那些已经有了自相矛盾种子的说法时，悖论才会出现。

有关这样的情形，正确的方法是换一种明智的说法，应该说“理发师为自己，还有镇上的每个人理发，除了那些自己为自己理发的人。”这样，悖论就不存在了。

还有另外一个悖论：某个实行专制统治的君主命令，穿过某座桥的任何人，都必须宣布他的目的地，以及他到那里去的目的。如果撒了谎，就必须被吊死。而如果说了真话，则可以保他平安无事。

一天有个人穿过这座桥，在被问及目的地时，他说道：“我要去往绞刑架，目的是被吊死”。

那么，如果他现在被吊死，他说的就是实话，就应该保他平安无事。然而，如果保他平安无事，他就说了谎话，就应该被吊死。如此反反复复，死循环下去。

这同样是，答案一定是可以预料到的，并且一定是排除在界限范围之外的，否者这项法令将毫无意义。（在真实生活中，我想象这个专制的君主会说“吊死他，因为他是个聪明的家伙”，或者说“要把他吊死他才会告诉我真话，这样你就可以确保他的尸体平安无事了。”）

在数学中，存在禁止悖论源头的倾向。例如，如果允许除以零，就很容易证明，所有各种数都相等。于是，为了防止这种事情发生，数学家们就武断地禁止除以零，如此而已。

数学中更精妙的悖论则有着它们的积极作用，因为它们刺激了人们的思想，并鼓励了数学严密性的发展。回到公元前450年，例如，希腊哲学家埃利亚的芝诺（Zeno of Elea）提出了四个悖论，它们都倾向于表明，正如所感觉到的那样，这些情况是不可能发生的。

其中最有名的一个悖论通常被称为“阿喀琉斯和乌龟”，这个悖论是这样的：

假设阿喀琉斯（参与过特洛伊之战的跑得最快的希腊英雄）能跑得比乌龟快十倍，并假设他们两个参加一次赛跑，让乌龟提前十码出发。

在这种情况下，出现的争论是，阿喀琉斯有可能超不过乌龟，因为在阿喀琉斯跑过他和乌龟原先位置之间的十码距离时，乌龟已经领先了一码。当阿喀琉斯再跑过一码时，乌龟又领先了十分之一码，而当阿喀琉斯又跑过十分之一码时，乌龟还是领先了百分之一码，如此永远继续下去。阿喀琉斯跑得越来越靠近乌龟，但是他永远追不上它。

推理是无可挑剔的，但我们所有人都知道，事实上阿喀琉斯会很快超过乌龟。实际上，如果有两个人，A和B，在赛跑，如果A能够比B跑得快（哪怕只是快一点点），那即使B提前非常多（但应该是有限的多）出发，A最终也会追上B的，只要双方都以恒定的速度，在无限延长的时间内奔跑。

那么就存在一个悖论，即逻辑推理显示阿喀琉斯不能超过乌龟，但简单的观察则显示他能够超过（事实上也会超过）。

这个问题两千年来难住了数学家们，部分原因是因为他们认为下列情况是理所当然的，即：如果你有一个无限数列，比如：10+1+1/10+1/100...，那它的总和一定就是无穷大的，而穿越由这些数字所表示的距离所花费的时间也就一定是无穷大的。

不过，最终数学家们认识到，这一十分明显的假设——一个无限的数集，无论它多小，它都一定有一个无穷大的和——是完全错误的。

在后来的研究中，大家又认识到，其实，对这样的无限数集的表达令人惊讶地简单。考虑数列10+1+1/10+1/100...，将10和1加起来，可以得到11；将1/10加在其上，可以得到11.1；将1/100加在其上，可以得到11.11；再将1/1000加在其上，可以得到11.111。如果你将此类数无限地加起来，就会得到11.111111...。但这样一个无限的循环小数正好是分数11-1/9（十一又九分之一）。

因此，表示乌龟领先阿喀琉斯距离的整个不断递减的无限数集，其总和也就只有11-1/9码，而阿喀琉斯要追上乌龟，只需要跑11-1/9码。

带有有限和的无限数列是“收敛数列”，而根据我的判断，其最简单的例子是1+1/2+1/4+1/8...，其中每一项都是前面一项的一半。如果你开始将这样一个数列的每一项加起来，你就会毫不费劲地说服自己，整个无限数集的总和只是2。

带有无穷和的无限数列则为“发散数列”。这样，数列1+2+4+8...明显会变得越来越大，且没有限制，以致于它的和可以被称为是无穷大的。

要想区分一个数列是发散的还是收敛的，并非总是那么容易。例如，数列1+1/2+1/3+1/4+1/5...是发散的。如果你将每一项加起来，它们的和会连续增大。不可否认，和的增长会变得越来越慢，但如果你取足够多的项，你就能够得到大于2、或3、或4，或者是你能说得出来的任何更大数的和。

我相信，这个数列也是我们可能得到的，最温和的发散数列。

· · ·

如果我没记错的话，在我中学的中级代数课程中，就学过了收敛数列的知识。当时我才十四岁，这真的让我感到很震惊。

不幸的是，我并不是个天生的数学家。有那么一些人，即使是在他们的青少年时代，就能够掌握精妙的数学关系——就像伽罗瓦（Galois）、克莱拉乌特（Clairaut）、帕斯卡尔（Pascal）、高斯（Gauss）他们一样——但我并非其中的一员，感觉和他们相差了好几个光年的距离。

我不停地与收敛数列做斗争，并试图以一种模糊的、不系统的方式来看待一些东西。而现在，半个世纪之后，我有了更多的经验，能够以更加明智的方式来表现那些少年时期的想法。

让我们考虑数列1+1/2+1/4+1/8+1/16...，并试图去找到一种更加直观的方式的表示它们。例如，设想一列正方形，第一个的边长为1厘米，第二个为1/2厘米，第三个为1/4厘米，第四个为1/8厘米，如此持续下去。

设想将它们紧紧地贴在一起，让最大的一个正方形在左边，第二大的正方形紧靠在它的右边，然后是第三大的、第四大的，如此持续。你就会得到一条由无限数量的越来越小的正方形紧靠在一起组成的直线。

将它们全部加在一起，记住是它们全部，将会延伸2厘米的长度。第一个正方形占了整个长度的一半，下一个则占了剩下长度的一半，再下一个又占了剩下长度的一半，如此永远持续下去。

自然，正方形很快就会变得极端的小。第二十七个正方形的边长大约只有一亿分之一厘米，于是让我们想象，将这个正方形以及其后的所有正方形放大一亿倍。第二十七个正方形的每个边长就会变成1厘米，紧跟着它的另一个正方形的每个边长就会变成1/2厘米，再下一个则为1/4厘米，如此持续。

简而言之，通过放大会产生一个，在尺寸和正方形数量上，与我们开始使用的数列正好相同的数列。

另外，第五十一个正方形已经小到只有大约一个质子的尺寸。不过，如果将其放大为1厘米的正方形，它还是会有一个在尺寸和正方形数量上与我们开始使用的数列正好相同的数列。

我们可以永远持续下去，绝不会穷尽。不管我们走得多远，哪怕是第数百万个不断变小的正方形，第数万亿个、第10的39次方个不断变小的正方形，我们都会得到一个与原始的那个数列完全相似的数列。这样的情形可以说展示了“自相似性”。

而将它们所有的、所有的加在一起，则会得到一个2厘米的宽度。并不是说2厘米宽度有什么魔力。我们同样也可以将其设计为1厘米宽度，或者1/10厘米宽度，或者是一个质子的宽度。

试图以1码等于36英寸这样简单的思路去“理解”这一点是没有用的。对于无穷量，我们并没有直接的经验，并且我们也不可能有。我们只能试图去想象无穷量存在的结果，而其结果与我们所能经历的任何东西都太不相同了，以至于它们“毫无意义”。

例如，一条直线上点的数量比整数的数量具有更高的无限性。没有现成的方法，可以让你去匹配这些点与数字。如果你试图将点按照数字加以排列，你总是会发现有些点上没有对应的数字。实际上，有无限多的点找不到与它们对应的数字。

另一方面，你可以将1厘米长的直线上的点，用另一条2 厘米长的直线上的点来匹配，这样，你一定会得出结论，较短直线上的点与较长直线上的点一样多。实际上，一条1厘米长的直线上的点可以多到挤满整个三维宇宙。你想要得到解释吗？我解释不了，任何人都解释不了。但可以证明的是，它不是能用普通的方式就可以“说得通”的。

· · ·

让我们再回到自相似性。我们可以发现，不仅在数列中，而且在几何形状中，都存在自相似性。例如，1906年，瑞典数学家赫尔格·冯·科赫（Helge von Koch）（1870-1924）创造了一种超级雪花。他是这样得到的。

从一个等边三角形（每个边都相等）开始，将每个边分成三等分，并在每个边三等分中间的一段上构造出一个更小的新的等边三角形，这样就可以得到一个六角星形，然后将六角星形的六个等边三角形的每条边分成三等分，并在每个边三等分中间的一段上构造一个小的新的等边三角形。现在，你就得到了一个由十八个等边三角形镶嵌成的图案。再将这十八个等边三角形的每条边分成三等分——如此持续，再持续，永远持续下去。

自然，不管初始的三角形有多大，你的绘图技巧有多高超，新的三角形都会很快变得很小而无法绘制。你不得不凭想象去绘制，并试图得出结果。

如果你一直将超级雪花构建下去，每一级包裹雪花的周长就会形成一个发散数列。因此，最终雪花的周长的长度是无穷大的。

在另一方面，每一级雪花的面积则会形成一个收敛数列，带有有限的总和。这意味着，即使到了最后，周长无穷大， 雪花的面积都不会超过初始等边三角形的1.6倍。

现在假设，你去研究初始三角形一个边上相对较大的三角形。它会是无限复杂的，因为越来越小、越来越小的三角形一直从它身上迸发出来，没完没了。但是，如果你取其中一个小得只能在显微镜下才能看见的三角形，并想象将其放大到便于观察的程度，它又会变得和较大的三角形一样的复杂。如果你考虑一个更小以及再小的三角形的话，其复杂程度永远都不会降低。超级雪花展示了自相似性。

下面是另外一个例子。设想有一棵树，将其树干分成三根树枝。又将每根树枝分成三根较小的树枝，再将三根较小的树枝分成三根更小的树枝。你可以很容易想象，一棵真树的树枝分布可能也会是这样的。

但是，要得到一棵数学超级树，你就必须想象，所有的树枝都在永远不停地分成三根更小的树枝。这样一棵超级树也显示出了自相似性，每根树枝，不管它多小，都与整棵树一样复杂。

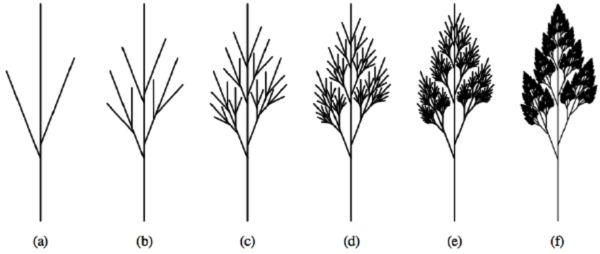
这样的曲线和几何图形最初被称为“病态的”，因为它们不遵守统治着普通几何的多边形、圆圈、球体和圆柱体的简单规则。

1977年，法裔美籍数学家贝诺特·曼德尔布罗特（Benoit Mandelbrot）开始系统地研究这样的病态曲线，并证明它们甚至不符合几何图形的最基本性质。

在我们开始接触几何学的时候，我们学到的都是，点是零维度的，直线的一个维度的，平面是两个维度的，而实体是三个维度的。最后，我们可能会学到，如果一个实体拥有持续的时间并在时间上存在，它就是四个维度的。我们甚至可能被灌输这样的观念，就是几何学家可以自然而然地解决更高维度的问题。

但是，所有这些维度都为整数——0、1、2、3等等。我们又怎么能够得到别的东西呢？

而曼德尔布罗特的研究结果表明，超级雪花的边界是如此的模糊，而且在每一点都有这样的急转弯，将其考虑为一般意义上的一条线是没有用的。它并不是一条线，也不是一个平面。它的维度介于1到2之间。事实上，曼德尔布罗特证明了，它的维度数等于4的对数除以3的对数。其结果大约为1.26186。因此，超级雪花的边界的维度数刚刚超过1-1/4（一又四分之一）。

其他这样的图形也有分数维度数，因此，它们后来被称为“分形”。

事实证明，分形并不是数学家通过狂热想象形成的几何形状的病态示例。它们比理想化的光滑、简单的曲线和平面等几何图形，更接近世界上的真实物体。而正是这些理想化的光滑、简单的曲线和平面，才是想象的产物。

因此，曼德尔布罗特的工作变得越来越重要了。

· · ·

现在让我们来稍微改变一下话题。几年前，我有机会偶尔去洛克菲勒大学，在那里我遇到了海因茨·帕格尔斯。他长着一头白发，有着一张和善、没有皱纹的脸，是个非常令人愉快和聪明的人。

他是个物理学家，对物理学的了解比我多得多。这并不奇怪，对于某个具体方面，每个人都比我知道得要多。而且，我还觉得他比我要聪明得多。

你可能会想，你同意我有一个巨大的自我，我会讨厌那些看起来比我更聪明的人，实际上并非如此。我发现比我聪明的人（海因茨是我遇到的第三个这样的人）都是非常友好和让人愉快的，而且我还发现如果我仔细去倾听，我会足以被激发出有用的想法；毕竟，想法就是我写作的话题。

我记得在我们的第一次谈话中，海因茨谈到了“膨胀宇宙”，这是一个新的想法，即宇宙在形成后的第一个瞬间就以巨大的速度膨胀，从而解释了一些困扰那些认为大爆炸的最初时刻没有膨胀的天文学家的一些问题。

特别让我感兴趣的是，根据这个理论，海因茨说宇宙是从真空的量子涨落开始的，因此它是被无中生有地创造出来的。

这让我非常兴奋，因为在《科幻和科学小说》杂志1966年9月刊（这还是在膨胀宇宙理论诞生许多年之前）中，我发表了一篇名为《我在查看四片叶子的三叶草》的短文，文中我认为宇宙是在大爆炸时被无中生有地创造出来的。事实上，短文的一个关键陈述是，我对我所谓的“阿西莫夫宇宙学原理”的定义——即“在开始的时候，什么都没有。”

这并不意味着我预见了膨胀的宇宙。我只是获得了这些直觉的推动力，但我缺乏执行的能力。因此，14岁时，有关收敛级数，我有了模糊的自相似性的直觉概念，但在当时，或者之后的任何时候，我都不可能复制曼德布罗特所做的工作。虽然我抓住了无中生有创造的概念，但就是再给我一百万年，我也不可能建立起膨胀宇宙的详细理论。（然而，我也并不是一个完全失败的人。我很早就意识到，我的直觉掌握能力，使得我能够去撰写科幻小说。）

此后，我会定期见到海因茨，在他成为纽约科学院院长后更是如此。

一次，我们一群人，包括海因茨和我自己，坐着讨论这样和那样的问题，海因茨提出了一个有趣的问题。

他说：“你认为，有没有可能，有一天科学上的所有问题都将得到解答，而再也没有什么可做的了？还是不可能解答所有的问题？”

“而现在我们能决定这两种情况中哪一种是正确的吗？”

我是第一个说话的人，我说道，“我相信我们现在可以做出决定，海因茨，而且很容易。”

海因茨转向我说，“怎么决定，艾萨克？”

我说：“我相信宇宙本质上具有非常复杂的分形特性，对科学的追求也有着共同的特性。这样，宇宙中任何未被了解的部分，和科学研究中任何尚未被解决的部分，与已被了解和已被解决的部分相比，无论多小，它们都包含着原始的复杂性。因此，我们永远都无法将其穷尽。无论我们走多远，前方的路还是会和开始的一样长，这就是宇宙的奥秘。”

我把这一切都告诉了我亲爱的妻子珍妮特，她若有所思地看着我说：“你最好把这个想法写下来。”

“为什么呢？”我说。“这只是个想法。”

她说，“海因茨可能用得着它。”

“我希望他能，”我说，“我没有足够的物理知识来做任何事情，而他能。”

“但他可能会忘记，他是从你那里听到的。”

“那有什么呢？想法很便宜。只有你用它们来做事，才会变得重要。”

· · ·

这样就来到了1988年7月22日，这天我和珍妮特前往纽约北部的伦斯尔维尔研究所，参加我们的第16届年度研讨会，这次研讨会主题是生物遗传学及其可能的副作用——科学、经济和政治方面的。

不过，其间又增加了一些额外的东西。马克·查特兰（Mark Chartrand）（几年前我在纽约海登天文馆担任馆长时遇到了他）是这些研讨会的常年教员，他带来了一盘30分钟的展示分形的录像带。

你看，就在过去的几年里，计算机已经变得足够强大，它可以生成一个分形图形，并慢慢地将其扩展数百万次。它们可以用非常复杂的分形来做到这一点，而不仅仅是像超级雪花和超级树这样简单（因此，也是无趣的）的东西。更重要的是，录像带用假颜色将其变得更加显眼。

我们在1988年7月25日星期一下午一点半开始观看录像带。

我们从一个黑色的心形图案开始，在它周围还有小的附属图案，它在屏幕上一点一点地变大。一个附属图案会慢慢成为中心并且变大，直到填满屏幕，接着又可以看到它又被附属图案包围。

其效果是慢慢陷入一种复杂，而这种复杂又一直不停地变得复杂。看起来像小点的小物体变得越来越大，在新的小物体形成的同时，又变得越来越复杂。这一直不停地持续了半小时，我们看到图案的不同部分不断扩展为美丽的新图案。

这绝对有催眠效果。我看了又看，过了一会儿，我根本无法收回我的注意力。整个过程就像我曾经经历，或可能会经历的无限，而不是仅仅是对它的想象和谈论。

播放结束后，回归现实世界却成了一种痛苦。

后来，我像在梦中一样对珍妮特说：“我相信那一次我对海因茨说的话是对的。就是宇宙和科学是-无穷尽的-无穷尽的-无穷尽的。科学工作永远不会全部完成，它只会越来越深入无穷无尽的复杂性之中。”

珍妮特皱起眉头，“不过你还是没有把那个想法写出来，是不是？”

我说，“是的，我还没有。”

当我们在研究所的时候，几乎与世界隔绝。没有报纸，没有广播，没有电视，而我们忙于研讨会的细节，对此并没有上心。

直到我们27日回到公寓，在我翻阅堆积起来的报纸时，才发现出了什么大事。

· · ·

当我们在伦斯尔维尔时，海因茨·帕格尔斯正在科罗拉多州参加一个物理扩大会议。帕格尔斯也是一个狂热的登山者，在7月24日星期天的周末假期，他和一个同伴爬上了14000英尺高的金字塔峰。下午一点半（就在我开始看录像带的24小时前），他在那里吃了午饭，然后开始下山。

他踩到一块松动的岩石，岩石抖动，让他失去了平衡。他从山坡上滚了下来，摔死了，才49岁。

在我翻到讣告页，看到这骇人的标题时，我完全没有准备。这是一个十分糟糕和意想不到的打击，如果不是珍妮特跑到我身后读这则讣告，恐怕我一定会痛苦地大叫起来。

我悲伤地抬头看着她，说：“现在他再也没有机会用到我的想法了。”

所以现在，我终于把它写好了。部分原因，是为了聊一聊我非常钦佩的海因茨。部分原因是我想把这个想法写在纸上，这样（只是可能），如果不是海因茨的话，其他人也可以用到它，并用它来做点什么事情了。

毕竟，我做不到。仅仅是获得这个想法，就已经代表了我的全部能力。在此之上，我一点也走不下去了。

（作者：艾萨克.阿西莫夫（Isaac Asimov），译者：劲松）