“握手”这件事，竟然可以用方程式来求解！

数学是一种语言，方程式是它的基本表达方式。我们都知道，宇宙的运行遵循某些规律。我们称之为科学，并用数学语言描述这些规律。这些规律用数学语言表述的话，就是方程式。世间万物，无论是星系的形成，还是孩子鼻子上的雀斑图案，都跟这些方程式有关。无论你喜欢与否，也无论你是个单凭感觉跃跃欲试的人，还是个在意秩序与细节的人，你生活的方方面面都由方程式主导着。方程式并不在乎你理解与否，依旧控制着你周围的一切事务。所以，是时候跟数学的世界变得更熟悉了。“握手”这件事，也可以用方程式来解答。

你是国家领导人峰会的官方摄影师， 也是捕捉拍摄对象最佳状态的专家。主办方要求你尽量多拍一些握手的照片。但这里有个问题，最后两位国家元首还有一个小时才能到场。这是一对自视甚高、哗众取宠的小丑。他们的发型让人摸不着头脑．政治立场更是可疑。其他100位国家元首中，没有一个愿意与他们握手。你知道一旦他们到达，所有元首都会停止握手。在这之前，你有时间拍下每一对可能握手的领导人照片吗?

握手问题在数学中是一个有着广泛研究的领域，其中十分出名的是各种各样又有趣的解决握手问题的方法。为了应对挑战，知道总共要拍多少张照片会十分有用。我们观察下面这几组人，看看他们需要握多少次手。

安娜问候鲍勃，那么目前只握了一次手。

卡拉来了。她需要与安娜和鲍勃握手，所以握手的次数增加了2 次。

迭戈来了。他需要与安娜、鲍勃和卡拉握手，所以握手的次数增加了 3 次。

当伊迪丝来的时候，她需要握 4 次手。依此类推。举个例，当第 25 个人来的时候，他需要和已在那里的 24 个人握手。第 n 个人必须与第 n - 1 个已到场的人握手。所以，要计算 100 个人需要握多少次手，你需要算出 1 + 2 + 3 +…+ 98 + 99。

在这里，你可以简单地花点时间用计算器，但是连续整数相加又是另一个古老的数学问题。解决这个问题的一种方法是用一些由点构成的三角形。如果你有五个人，你需要握 1 + 2 + 3 + 4 次手，你可以用一个三角形的点阵来表示：

你想要得到三角形内点的数量的公式。

矩形中的点的数量比较容易计算，所以，如果你再加上一个由相同数量的点组成的三角形，你就得到了一个宽 4 点高 5 点的矩形。

矩形中有 4 × 5 = 20 个 点， 这意味着每个三角形中必须有20 ÷ 2 = 10 个点。归纳一下，你可以看到如果三角形有 r 列，由两个这样的三角形组成的矩形就会有 r + 1 行。这意味着矩形中有 r ×（r + 1）个点。为了算出原来三角形的点的数量，你必须把这个减半，得出公式：

数学家十分熟悉该公式，也很了解其中的故事。在 18 世纪晚期，德国数学奇才卡尔·高斯（Carl Gauss）还是一名小学生时，他的老师给他布置了一个任务：把 1 到 100 的所有数字相加。传说高斯发现了这个捷径，并当场解决了这个问题，这让他懒惰的老师既气恼又尴尬。高斯后来成了最伟大的数学家之一。

对于 n 个人握手，你需要握 r = n–1 轮，因为你要使握手的轮数比总人数少 1。将公式中的 r 替换为 n–1，得到：

结果等于 4,950 次握手。拍这些照片，每张照片预计只需10 秒，但总共要花 49,500 秒，也就是 13 小时 45 分钟。所以没有办法在一小时内拍完所有的照片。但是会议中心请你来，并不想听你表示无能为力。让我们来看看你能做些什么。

刷新世界纪录的总统

在 1907 年的元旦，美国总统西奥多·罗斯福在白宫举行了一个开放日，公众可以来和他们的领导人见面。到白宫大门关闭之时，罗斯福已经和 8,513 个人握手了。这创下了单日握手次数最多的世界纪录，这一纪录保持了近 60 年。最长的握手纪录是两对被称为“握手族”的人士 2011 年创下的，他们在 33 小时 3 分钟之后才停止握手。

假设一开始你为各国元首第一轮握手都拍了一张照片。100 个人的话，就是 50 次握手，这将花费 500 秒的时间来拍摄。那么让我们看看你能在剩下的时间里给多少人拍完整的照片。拍照的时间是握手次数乘以 10 秒，所以：

你有 1 小时，也就是 60 × 60 = 3,600 秒。我们已经用了 500 秒，确保每个人都有至少一张照片，还剩下 3,100 秒。你需要求解的方程是： 3,100 = 5 （n–1）n

首先，方程两边同除以 5：

620 =（n–1）n

然后展开括号：

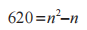
这种方程称为二次方程，因为未知数 n 是平方的形式。这种方程不像线性方程那么容易解，但如果你把方程变成一边等于零的形式，你可以使用二次方程求根公式（见绪言）。为了让我们的方程变成一边等于零，则方程两边同时减去 620：

得数应为正数且保留至小数点后一位，得出 n = 25.4。这意味着你可以拍下 25 个人握手的照片，需要 5 × 24 × 25 = 3,000 秒。这还给我们预留了 100 秒的时间，你可以用这点时间再拍 10 张照片，或者擦擦你额头上的汗。

你可以用图来表示所有国家元首握手的情况。如果你把 100 位国家元首当作一个圆周上的点，用点与点之间的连线来代表握手，你会得到一个复杂的图。此图名为“神秘玫瑰”，也许是因为它看起来有点像老教堂里那种圆形玫瑰彩色玻璃窗。真正让人感到不可思议的是，虽然事实上，这个图完全是由直线构成，但它看上去似乎有同心圆和曲线。下图是 25 人之间握手的玫瑰图，由爱德华·普拉特（Edward L. Platt）在其个人网站的神秘玫瑰生成器制作。

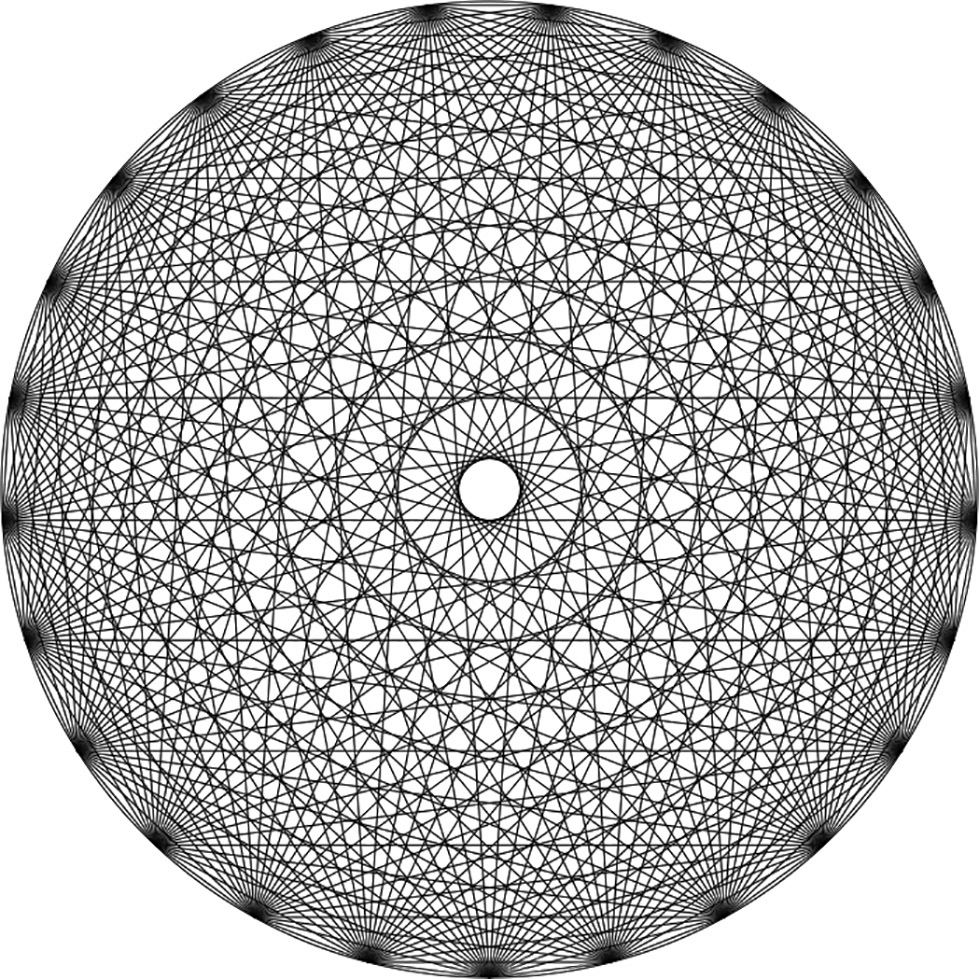
神秘玫瑰对你的问题并没有什么帮助，但它看起来确实很棒。

主办方对你的解决方案很满意。当一架引人注目的大型直升机和一队豪华轿车停在会场外的时候，你的任务也刚好完成。

延伸阅读：《方程式之美：隐藏在万事万物背后的数学公式》