高俊科趣谈无理数e(九-4)这些大学教材中关于连续(复利)计算公式的讲述错在哪里(例4)

(九-4) 这些大学教材中关于连续(复利)计算公式的讲述错在哪里(例4)

(题注：本《趣谈》一一分析这些大学教材中的错误，应当说做的是不受欢迎的事。

不过也只能这样做，雅各布.伯努利提出的这种错误的“连续(复利)计算”存在时间太长了，我从1988年在《数学的实践与认识》上发表文章《关于所谓增长率的连续计算问题》指出这种连续(复利)计算是错误的，到现在已经30多年了，这错误依然在大学教材中广泛存在，这种错误不是哪几家出版社的错，这错误在所有谈及这问题的书籍中都存在，在1997年诺贝尔经济学奖奖项中存在，不一一分析这些教材中的问题，很难让人相信这种连续(复利)计算方法是错误的，很难改正这种让学生们继续学习糊涂知识的局面，这就是我们要在这里多角度地、反复地、不厌其烦地一一分析这些教材中的错误的想法。)

本篇说一个金融学教材中怎么讲连续复利计算的例子。2007年清华大学出版社出版的一本《金融学》中以APR(年度百分率)表示一年分m期计算复利的名义年利率，以EFF表示有效年利率，接下来分析例5.1是怎么错讲连续复利计算模型的。

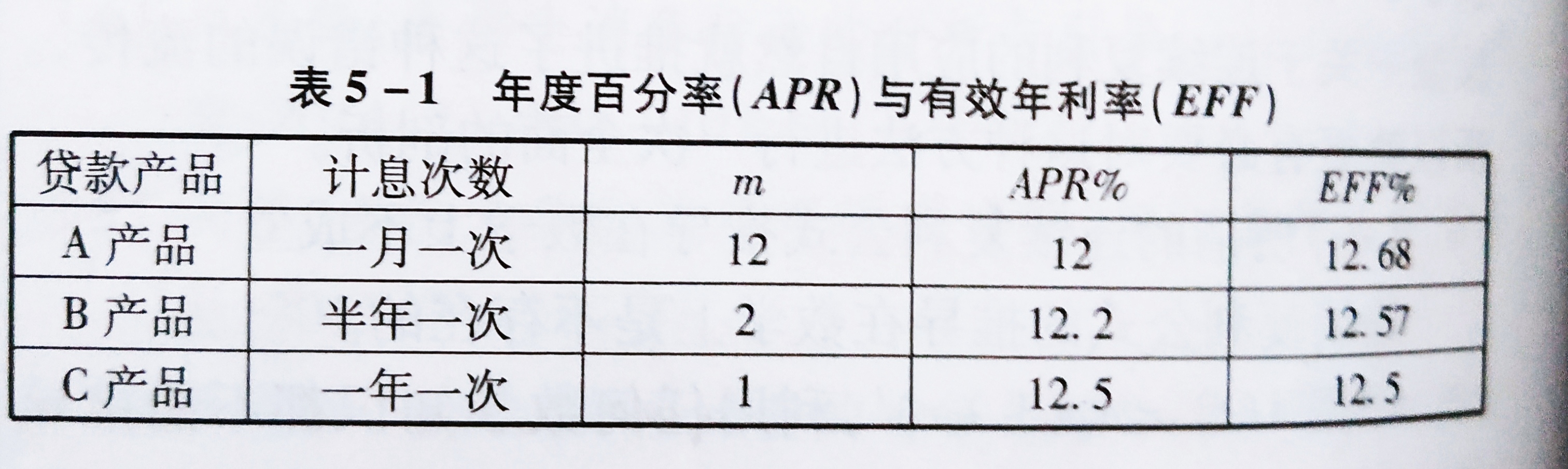
“例5.1 假定你想向银行申请一笔1年期贷款10000元，银行提供三种产品供你选择：A产品是每月支付一次利息，年利率(年度百分率)12%; B 产品是每半年支付一次利息，年度百分率12.2%;C产品是贷款到期时一次性支付利息和本金，年利率12.3%.这时你应究竟该选择哪一种贷款产品呢?当然是选择利率低的产品，但不是年度百分率，而应当看有效年利率孰高孰低。

对于年度百分率和有效年利率，二者有如下关系： 1＋EFF=(1＋APR/m)^m (5-5)

其中，EFF表示有效年利率，APR表示年度百分率，m表示每年计息次数。

运用上述公式，我们计算A、B、C三个贷款产品的有效年利率，计算结果见表5-1。从表5-1可以看到，C产品有效年利率最低，即该种贷款对借款人而言成本最低，所以应当选择C产品。

当每年计息次数m趋于无穷大时，即连续不断地进行复利时(连续金融概念)，有

1＋EFF=lim(1＋APR/m)^m=e^(APR) (5-6)”

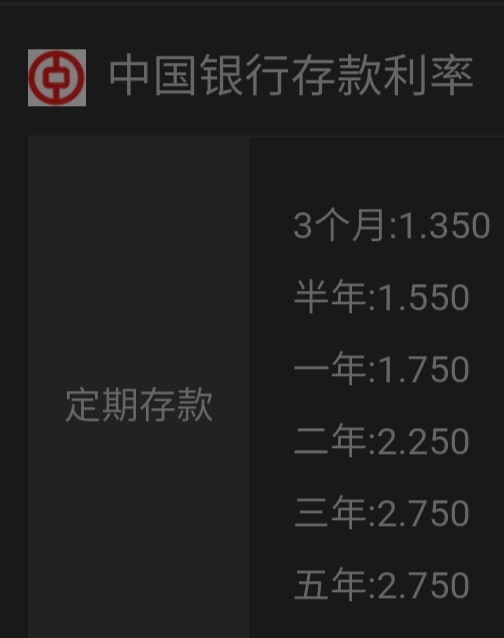
至此先不要看下面内容，结合当前中国银行现行储蓄利率表自己思考一下，这里讲的“连续不断地进行复利(连续金融概念)”是对还是错?

这本《金融学》中讲公式(5-5)和表(5-1)是从数学式和贷款应用两方面讲“当每年计息次数m趋于无穷大时，即连续不断地进行复利时(连续金融概念)”的合理性。

问题是，无论是在银行贷款还是在银行储蓄中，当一年中的计息次数m变动时，公式(5-5)中的APR是固定值，还是随一年中的计息次数m变动?

如果公式(5-5)中的APR是固定值，就说明这公式(5-5)与银行贷款和银行储蓄中的实际应用不是一回事，与实际计算相悖，“当每年计息次数m趋于无穷大时，即连续不断地进行复利时(连续金融概念)，有 1＋EFF=lim(1＋APR/m)^m=e^(APR) (5-6)”说不通;

如果公式(5-5)中的APR随m变动而变动，则“当每年计息次数m趋于无穷大时，即连续不断地进行复利时(连续金融概念)，有

1＋EFF=lim(1＋APR/m)^m=e^(APR) (5-6)”

如此，这极限式e^(APR) 中的APR就不是前边的值了，这APR就不知道会变成什么数值了，这极限式(5-6)没有意义。

就是说，无论怎么讲，这种“连续不断地进行复利时(连续金融概念)”都不成立。

本《趣谈》前面二至五已有论述：资金自身增值规律就是随时间连续“利生利”，即连续随时间按指数函数规律连续复利;资金借出方借入方都是按连续复利 ，即按指数函数规律思考问题。

这里的贷款年利率表(5-1)再次说明，银行与贷款人双方都是运用复利方法思考问题，这复利方法对年、对半年、对月一样，对更短的时间也是一样。就是说，双方都用的是连续复利计算，与资金增值规律一致。复利公式A。(1＋r)^t本身描述的就是资金增值规律，就是资金按连续复利呈指数函数增值的规律，不应当存在，也不存在另外的连续复利计算和概念。

问题：1997年诺贝尔经济学奖得主与人合著的《金融学》能不能正确讲述这种连续复利计算公式?这《金融学》有中译本，见下面图片;在1997年诺贝尔经济学奖奖项“B-S期权定价模型”中能不能正确应用这种连续复利计算公式?