剖析雅各布.伯努利一影响深远的方法错误──兼谈无理数e的秘密(前言)

剖析雅各布.伯努利一影响深远的方法错误──兼谈无理数e的秘密(前言)

数学大家雅各布.伯努利成就辉煌，贡献卓著，影响深远，世人敬仰；同样，雅各布.伯努利提出的很基础的、似是而非的错误方法也影向深远，且很难改正。雅各布.伯努利提出的很基础的错误的连续(复利)计算)在数学科普读物中存在，

在多门大学课程教材中存在，在1997年诺贝尔经济学奖获奖项目B-S期权定价公式中存在。

仅我们查看到过的国内外错误讲授这方法的教材就有800多种。

盲信权威的每一句话，雾里看花，把“似是”当成“是”，这就是这错误长期存在的原因。

一 盲信权威，雾里看花，把联想当数学推理，把“似是”当“是”，导致对这种连续(复利)计算被错误讲述、错误解释和错误应用。

二 这些科普读物中都讲连续(复利)计算外、还都讲无理数e和欧拉公式的神秘。盲信权威，雾里看花，把“似是”当“是”，这就产生了对无理数e和欧拉公式(也称为上帝公式)e^(iπ) 1=0 的神秘感。我们将给出分析 ，比如所称上帝公式e^(iπ) 1=0 ，就像求得余弦函数一个值cosπ=-1再得cosπ 1=0一样，求得指数函数一个值e^(iπ)=-1，就得到e^(iπ) 1=0 ，这里没有任何神秘。

三 盲信权威，雾里看花，把“似是”当“是”，也就导致了“似懂非懂”。对不同学科中的相对增长率、连续复利率、瞬时增长率、利息力、利息强度等概念从没有得到简单清晰正确解释。比如把“瞬时增长率”解释为“种群在任意小的时间段内的增长率”，

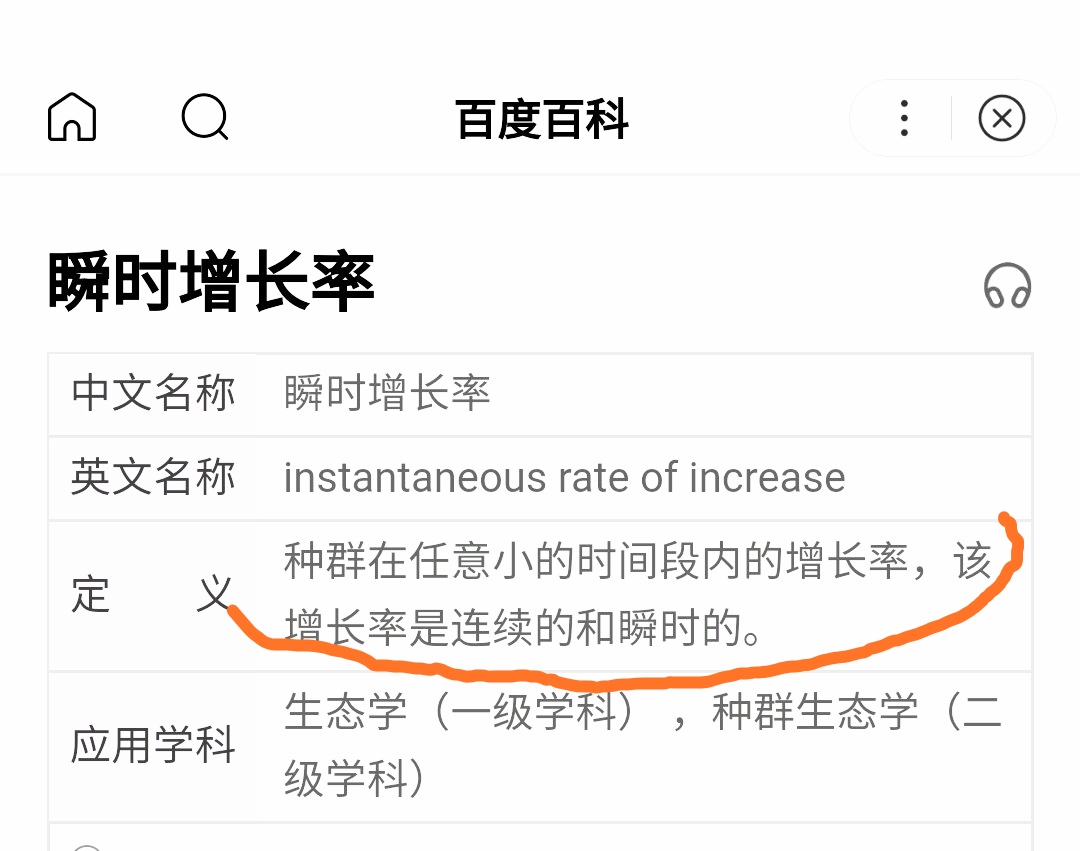这解释本身就是错误的，根本不能让人理解这概念说的是什么。我们在后边将分析指出，这些不同学科中的概念在数学上是同一数学参数，在各自领域都应有简短、清晰、准确的文字解释。

我1983年在学校内刊《河北电大》(经济版)上发的文章《一道习题的剖析》、

1988年在《数学的实践与认识》上发的文章《关于所谓增长率的连续计算问题》、

1998年在《数理统计与管理》上发的《关于复利率的连续计算方法–析国内外经管类数学教材中普遍存在的一种方法错误》、

2018年在《金融经济》上发的《连续复利错误面面观》

都是专论中这一方法错误的，可这错误依然在多门课程教材中存在，足见这方法在不少人的脑海里根深蒂固，不可动摇，也就很难改正。盲信权威，雾里看花，从数学构成上论述这方法错误，就有人从似是而非的应用上进行反驳；分析了在这领域中的应用错误后，就又有人从另一领域提出似是而非的应用进行反驳，这些反驳这也就促进了我进一步的深入思考。

为全面认识、改掉这一错误方法，就不得不从方法构成、解释、应用等各方面不厌其烦地一一进行分析。这就是我做这讨人嫌的事，一一批驳这些教材中的论述、撰写本系列文章的想法和原因，欢迎共同讨论。

本系列文章重新整理了一下以前发表在杂志和网络上的文章，包括此前发在《科普中国》上的文章，加上最近新的认识综合在一起发在这里，这些内容很基础、浅显，拟发章节目录如下：

一 怎么理解年增长率概念

二 资金自身增值就是随时间连续“利生利”即连续复利

三 借出方借入方都是连续复利思维，双方思维与资金增值规律一致

四 借出借入双方同意的利率由资金供求关系决定，围绕资金价值上下波动

五 日常用单利表达是因为单利简单、方便，支撑单利表达方法的还是复利即连续复利

六无理数e的来历──雅各布.伯努利在数学领域的历史性贡献

七 只用中学知识看雅各布.伯努利提出的“连续复利法”错在哪里

八 连续复利计算模型错在哪里──错在多侧面的混乱

九 (1)这部1982年版《经济数学基础(微积分)》中关于“连续(复利)计算”的讲述错在哪里

九 (2)这部1995年版《微积分教程》中关于“连续(复利)计算”的讲述错在哪里

九 (3)这部《微积分(上)》中关于“连续(复利)计算”的讲述错在哪里

九 (4)这部《金融学》中关于“连续(复利)计算”的讲述错在哪里

九 (5)这部《高等数学》中关于“连续(复利)计算”的讲述错在哪里

九 (6)这部美国人编著的《微积分及其应用》中关于“连续(复利)计算”的讲述错在哪里

十 (1)这部1984年版《管理数学》中关于“连续(复利)计算”的解释错在哪里

十 (2)这文章《关于复合总额计算模型》中关于“连续(复利)计算”的解释错在哪里

十 (3)这部《微积分》中关于“连续(复利)计算”的解释错在哪里

以下待定

十 (4--10)解释错

十一(1--6)(应用错误)