剖析雅各布.伯努利一影响深远的方法错误 十(5)

十 (5)这些美国人编著的《公司理财》中关于连续复利计算模型的解释错在哪里？

(题注(这题注说的是事实，用语尖刻一点是为了引起人们的重视)： 雅各布.伯努利把联想当推理，给出了错误的“连续复利法”。世人盲信权威，雾里看花，把“似是”当“是”；人们盲从潮流 ，单向思维，认“不是” 为“是”，于是就臆想出了对这种连续(复利)计算的多种错误讲述，编写出了种种错误解释和错误应用，以致这一错误方法广泛存在而不能改掉，为推动尽早改变这一现象，就必须一一剖析这些教材的讲法错在哪里，这不是教材编著者哪几位个人出现的错，1997年诺贝尔经济学奖奖项中也存在这错误，这说明1997年诺贝尔经济学奖评委会也没有看出这错误。)

关于连续复利计算模型的通常讲法是：

设初始资金是A。，年利率是r,于是就有t年后的资金总额公式 A。(1＋r)^t (1)；

如果一年中计算m次，每次利率为r/m，就有复利分期计算公式A。(1＋r/m)^(mt) (2):令m趋于无穷大，得连续复利计算模型A。e^(rt) (3)

​2009年机械工业出版社出版的美国人斯蒂芬 A 罗斯、伦道夫 W 维斯特菲尔德、杰弗利 F 杰夫编著的《公司理财》(第八版)中文翻译本在讲了连续复利计算公式后在第61页给出如下例题：

​“例 4-15 连续复利 Linda Defond 以连续复利计息方式将其1000美元投资1年，那么，她的投资到了年末将等于多少?

由式(4-9) (指该书中公式C。e^(rT) ，即本文中的公式(3) ) 可得

1000美元xe^0.10=1000美元x1.052=1105.20美元这一结果也可很容易地从表A-5中查到，即只要在横栏中找出所给的利率r=10%，在竖栏中找出T，与本例有关的表中的部分为

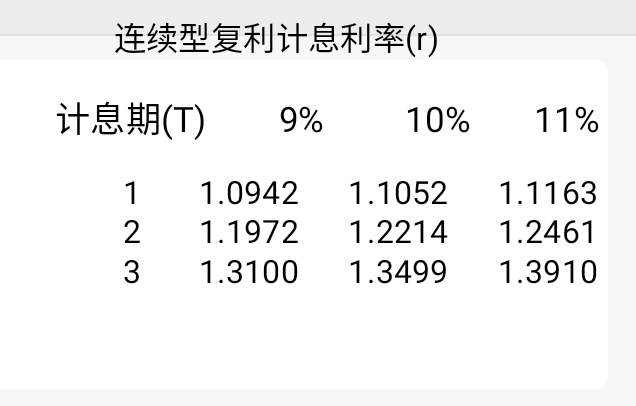注意利率为10%的连续计息等价于利率10.52%的利率的年复利计息方式。换句话说， Linda认为将她的资金以10%的利率连续计息或是以10.52%的利率年复利是没有差别的。 ”

我们​应当能理解到，这里所说的 “Linda认为”是对的，不管解释为离散计算还是解释为连续计算，不管是否“计息次数增加到极限情况”，也不管是否“资金在每一瞬间都会被用来再投资”，就像0.75=3/4一样，等式 A。e^(0.1t)=A。(1＋ 10.517%)^t 恒成立，A。(1＋r)^t=A。e^(txln(1＋r))=A。e^(Rt)恒成立，R=ln(1＋r). 在这恒等式中，r的含义前后一样，r和R的含义不一样(今后我们将专篇分析这两个字母r与R的关系和各自的经济含义)，以此正好揭示由A。(1＋r)^t不能推导出A。e^(rt)，由A。(1＋r)^t推导A。e^(rt)是错误的。可惜的是，这部《公司理财》中没有据此进一步去揭示连续复利计算公式构成错误，反而在该书第72页论述这种连续复利计算时说，“计息次数增加到极限情况就是连续复利计息，其资金在每一瞬间都会被用来再投资。”

​就是说，这教材已说到“Linda认为将她的资金以10%的利率连续计息或是以10.52%的利率年复利是没有差别的”， 但没有接下来说明这“Linda认为”是对还是错，没有向前进一步去分析为什么会有这“Linda认为“? 无视这需要探究的问题，反而退回来又以脱离实际的臆想从正面去解释错误的连续复利计算公式，这解释也就照样错了。