剖析雅各布.伯努利一影响深远的方法错误十(7) (高俊科)

十 (7)这部《工程经济学》中关于“连续(复利)计算”的解释错在哪里?

首先说明，长期广泛存在的这种连续复利计算方法是错误的，这不是哪个教材编写者个人的错，也不是哪家出版社的错，我国出版的各种教材中的这种方法90%以上来自美国教材，1997年诺贝尔经济学奖奖项中也存在这错误，这种错误方法存在根深蒂固，全面认识这错误就需要对这各种错误讲法、错误解释和错误应用一一进行分析。

2004年清华大学出版社出版的一部《技术经济学》第49第50页中也讲了这种连续复利计算。

“3 连续复利

设r为一期(通常指一年)的名义年利率，一年计息m次，则计息期利率

i=r/m (3-6)

i(实)=(1 r/m) ^m-1 (3-7)

当m趋于无穷大时有

i(实)=lim((1 r/m) ^m-1 )

=lim(((1 r/m) ^(m/r))^r-1 )=e^r-1 (3-8)

下面以12%和24%的名义年利率为例，计算比较名义利率、实际利率以及连续复利，结果如表(3-6)所示。

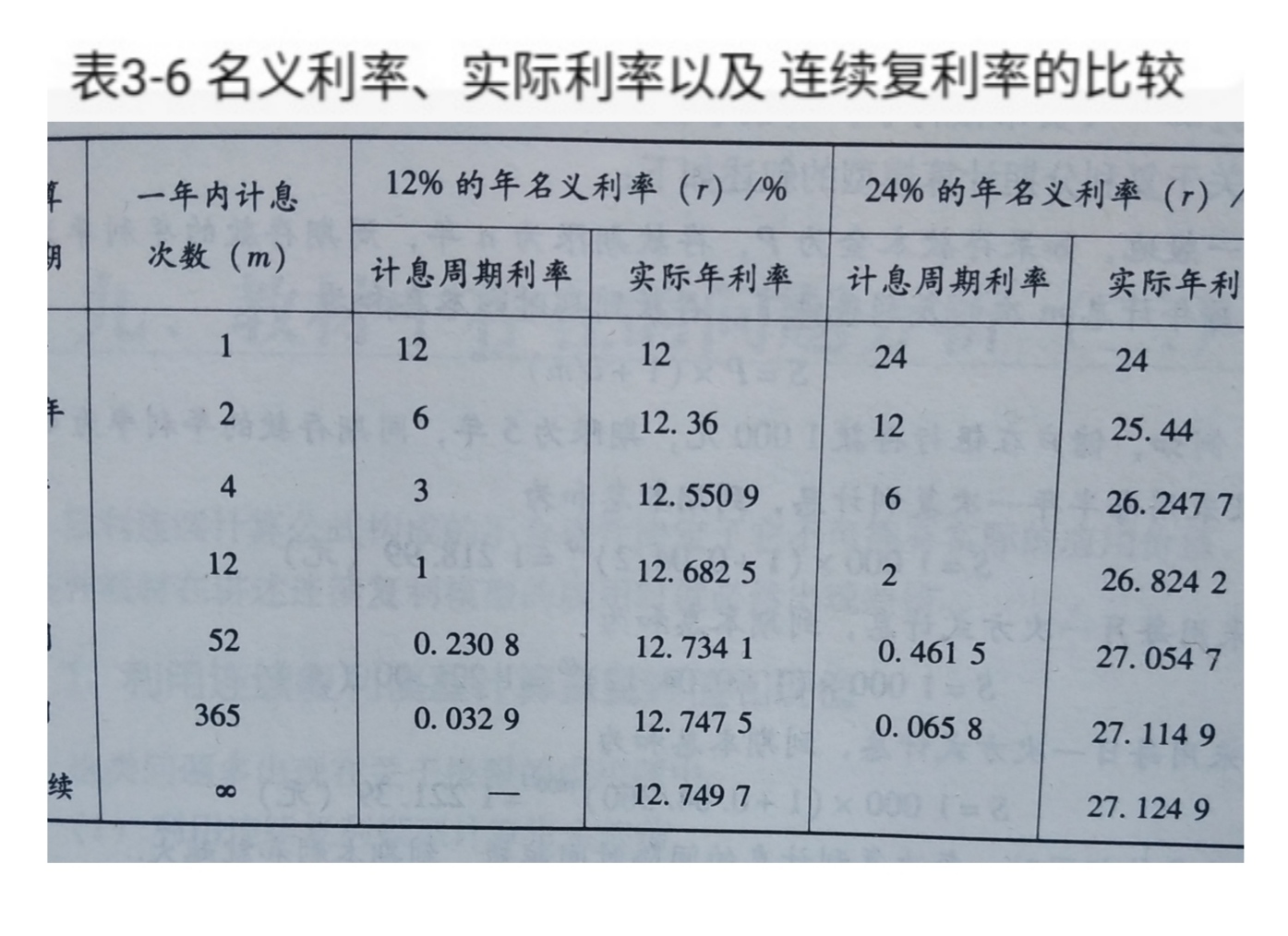(注：这图片为原书内容，这图表由本人重新制作)

从上述结果分析：实际利率与名义利率的差异随着计息次数的增大而增大，差异最大值为连续复利率之差，当计息次数大于1次时，在相同的计息次数下，实际利率与名义利率的差异随着名义利率的上升而增大。此外，连续利率与按日进行复利计算的实际利率是很接近的。实际上，当名义利率不很大时，计息次数从365增加到无限大，其实际利率增加的值是微不足道的。 ”

这段关于连续复利计算的解释错在哪里?不究其义，这一句一句的叙述都应该是对的，细究起来，这叙述都是不对的。

一 注意，在(3-7)式中的r的概念就是糊涂的。

无论中国银行储蓄还是贷款工作中，计息期改变，也就是一年中计息次数m改变，相应的名义年利率r的数值一定改变。同样，在其它任何应用中也必定是这样，只要是一年中的计息次数m改变，相应的名义年利率r的数值一定改变。m不同，字母r表达的含义不同，(3-7)式中,m可以有无数种取值，也就是说，r表达了无数个概念，这样的(3-7)式构成无道理。(3-7)式与(3-8)是两个不同的式子，两者不存在推导关系。

二 (3-7)在金融领域没有任何应用，在其它任何领域也都没有应用(谁能列举出来一个应用实例?)。

表(3-6)与式(3-7)作用一样，都仅仅表达了数列(3-7)是一个单调递增数列。

三 公式是否表达连续计算，由事物本身特性决定，不能由是否采用无理数e表达决定，比如说，

A。e^(0.0953t)=A。(1 10%)^t都可以表达离散计算或连续计算。这一段最后一句说“实际上，当名义利率不很大时，计息次数从365增加到无限大，其实际利率增加的值是微不足道的。 ”只是从纯数学上说明(3-7)存在极限而已，不说明其它任何问题。

本篇仅说了三个方面，这里不做过多分析了，有兴趣详看的朋友可看第八篇。

总之，这《技术经济学》中在这里用的名义年利率概念是模糊的，或说是错误的。分段看段内容的语句是对的，但表达的意思与连续复利计算模型的构成无关，一点也没有解释到这种连续复利计算模型的合理性。

从表达连续复利计算模型的意义上讲，这里的解释不成立，是错误的。因为连续复利计算模型本身就是错误的，对错误的知识本不存在正面解释。