十(8)这部《高等数学》是怎么错误解释连续(复利)计算的---剖析雅各布伯努利一影响深远的方法错误

剖析雅各布伯努利一影响深远的方法错误

十(8) 这部《高等数学》是怎么错误解释连续(复利)计算的-

2009年机械工业出版社出版的一部《高等数学》中按通常讲法讲连续(复利)计算的叙述是：其他许多问题，如细菌(生命细胞)的繁殖、放射性元素的衰变都涉及n→∞时p=p。(1＋r/n)^(nt )的极限问题，求极限得到得出p=limp。(1＋r/n)^(nt )=p。e^(rt )

随即给出结论(该书34页)：“这就是工程应用中为什么指数(或对数)函数取e为底的缘故”。

这里仅以细菌日繁殖率r=100%为例分析一下这种连续(复利)计算方法错在哪里?

一 在n=1时p。(1＋100%)^t 中r=100%表达的是经过一天细菌数量翻一翻。仔细考虑一下可知，在n=2时p。(1＋100%/2)^(2t) 中r=100%的含义已经改变了，就需要赋予r=100%新的解释。在n=3时p。(1＋100%/3)^(3t) 中r=100%的含义就又改变了。作为应用，p。(1＋r/n)^(nt )中同一个字母r的含义都是不固定的，同一字母的含义一直在改变，这公式的构成就陷入了错误思维。

二 无论是t取整数还是连续实数，无论是所谓连续计算还是离散计算，在描述这细菌繁殖规律上，这四个指数函数p。2^t、p。(1＋100%)^t、p。5(3＋(-100%))^t、p。e^(txln2)等效，就是都是只含一个参数的指数函数p。a^t、p。(1＋r)^t、p。(3＋b)^t、p。e^(Rt)等效，就是说，细菌(生命细胞)的繁殖、放射性元素的衰变本身不涉及n→∞时p=p。(1＋r/n)^(nt )的极限。

我们以后会讲，指数函数p。e^(Rt )如同p。(1＋r)^t 一样，有特别意义的应用，这是数学方法问题，而连续复利计算方法是错误的。。

用于表达这细菌日繁殖率r=100%的应用，p。e^(Rt )中的R=ln2，而不是R=100%，仅凭这一点，就能充分揭示连续(复利)计算的荒谬。

三 由这种荒谬的所谓连续(复利)法的计算衍生出来的是一些含糊概念，如金融学中的连续复利率、生物学中的瞬时增长率，细菌日繁殖率为r=100%时，每小时的繁殖率就是(1＋100%)^(1/24)-1=2.930%，每秒中的繁殖率就是(1＋100%)^(60x60x(1/24))-1=0.0286%，按此理解，无限短的时间的增长率就是0.

而各种教材中的解释“瞬时增长率”为“种群在任意小的时间段的增长率”，见下面百度百科解释

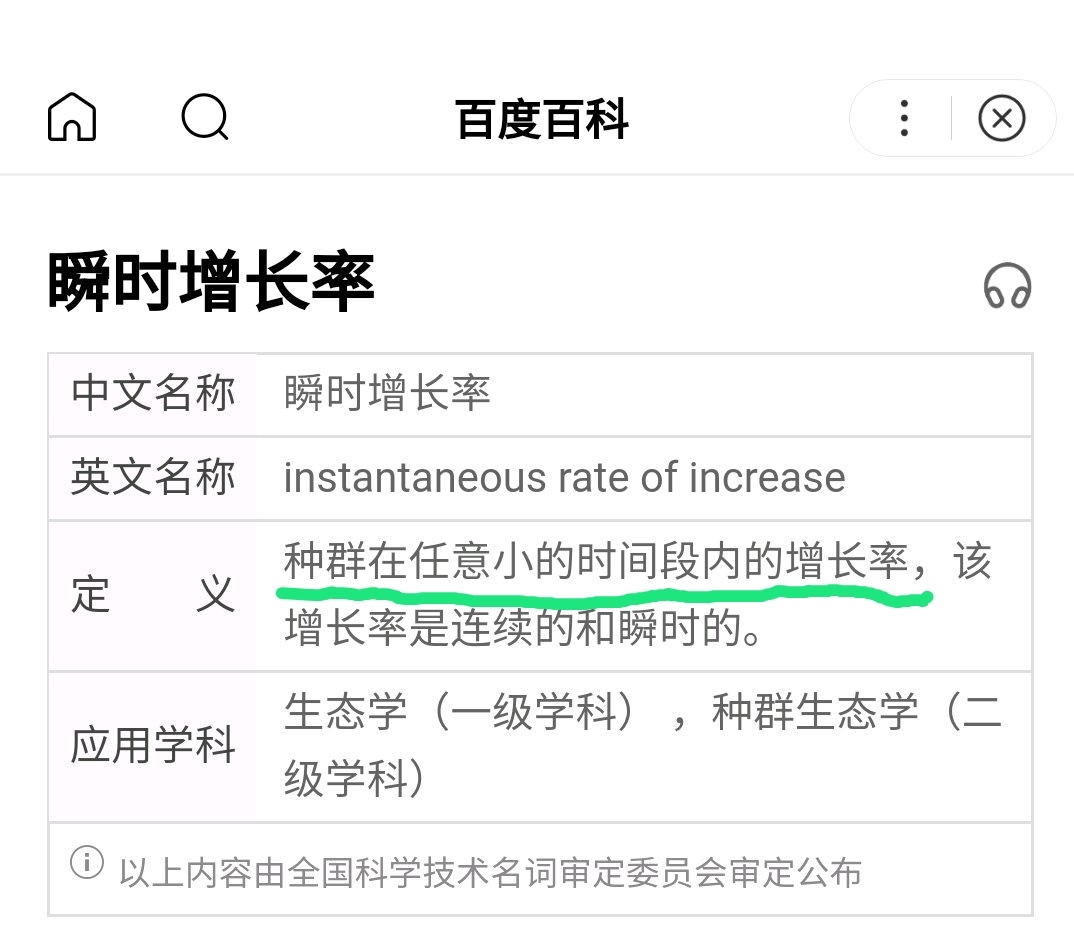我们以后的文章会给出具体分析，这些概念可用简单、明确、清晰的语言解释，但现在的解释都是含混的。

总之，雅各布伯努利提出的连续“复利”计算方法是错误的，这错误存在广泛，还影响到对所谓的“连续复利率”、“瞬时增长率”、“利息强度”等概念解释和理解。许多人根本没有理解这种连续(复利)计算方法到底是怎么回事，人云亦云，当然，这不是哪几部教材中的问题，1997年诺贝尔经济学奖评委会也没有看到这错误，见下面文章摘要。