“简单”的数学未解之谜

很久没有聊数学了，今天我们搞点轻松的话题，这就是数学中的未解之谜，听到这个题目，你可能首先就会想到黎曼猜想、想到哥德巴赫猜想、ABC猜想等等，这些玩意儿都何其高深，我TM还是关了吧，不听刘夫斯基吹牛X了。但是不要慌，我们今天要说的这几个数学未解之谜，小学生都能看得懂，你要就是小学没毕业，那就算了吧，别难为自己。不过，虽然看起来很简单，但它们的难度却丝毫不亚于哥德巴赫猜想这样高端的问题，在数学史的长河中，一代代数学家前仆后继，至今也没得出个所以然来。我大致整理了一下，今天我们就来个简单的盘点。

第一个问题是3x+1问题。

这个问题的表述是这样的，说从任意一个正整数开始，重复对其进行这样的操作，如果它是偶数，那就把它除以2，如果它是奇数，那就是乘3再加1。那么经过这么一番折腾之后，我们是否总是会得到序列4,2,1,4,2,1...这种循环呢？

什么意思呢？我们举个例子，拿出一个正整数比如说28，是偶数，那就除以2变成了14，还是偶数，那就再除以2变成7，这下就是奇数了，所以用3×7+1，结果是22，接下来持续操作，我们就会得到这样的序列：

11,34,17,52,26,13,40,20,10,5,16,8,4,2,1,4,2,1...然后就开始循环了。

你可以随便找正整数，我相信你都会得到这样的结果，那么是不是对于所有的正整数来说，都是如此呢？这个问题看似很简单，但却折进去了很多数学家，我们从这个问题名字的演变就能看出端倪，比如这个问题有这么一大堆名字：科拉兹猜想、叙拉古问题、角谷猜想、哈斯算法、乌拉姆问题等等，后来实在太乱套了，索性就直接叫3x+1问题了。总之关于这个问题，至今没有答案。你要是真的找到了一个例外，那你肯定名垂数学史了。

第二个问题是196问题。

这是一个关于回文数的问题，回文数很简单，正读反读都一样的书就是回文数，比如181,343等等等等。现在你随便选个正整数，不断把它加上反过来写的数，那么到最后你是不是一定可以得到一个回文数呢？我们来试一下，比如69。

69+96=165；

165+561=726；

726+627=1353；

1353+3531=4884。

妥了，仅仅四步运算，我们就得到了一个回文数。你自己随便试，可能有些数字需要运算很多步，但最终你都会得到一个回文数。直观地看，一个数我们不断地一正一反加下去，肯定会得到一个回文数，计算机在那嗷嗷算，发现也没毛病。但这其中有个例外，而且令人费解的是，这个例外并不是一个什么好几万位、好几十万位的大数，而是169，现在数学家们已经利用计算机算了好几亿步了，但还是没有产生回文数。那么169到底能不能产生回文数呢？如果不能，该如何证明？如果能，它到底需要多少步？为什么它就这么特殊？这个问题，至今无解。

第三个问题是吉尔布雷斯猜想。

提出者自然是一个名叫吉尔布雷斯的数学家，有一天这哥们在餐厅等菜，无所事事之下，这哥们拿起了餐巾纸，在上面写下了质数数列：

2,3,5,7,11,13,17,19,23,29,31...

然后他求出了相邻两项的差，结果为：

1,2,2,4,2,4,2,4,6,2...

继续这一操作，再得出一个新的数列：

1,0,2,2,2,2,2,2,4...

重复进行下去：

1,2,0,0,0,0,0,2...

只要你有时间，随便造。最后我们会发现这样一个规律，那就是每行序列的第一个数都是1。有了这个发现之后，吉尔布雷斯感觉很有意思，于是他让他的两个学生检验一下，果不其然，这哥俩算到了第64419行时，数列的开头也仍然是1，但怎么证明，这师徒三人却没有思路。于是在1958年，吉尔布雷斯在一个数学交流会上提出了他的发现，吉尔布雷斯猜想由此诞生。当然了，肯定有人是不信邪的，于是在1993年，一位名叫安德鲁-奥德里兹科的哥们一口气算到了第3460多亿行，结果还是没有出现例外。那么这是否是一个铁律呢？目前还没有得到证明。

第四个问题名叫辛马斯特猜想。

这次要用到的工具就是我们十分熟悉的杨辉三角，也就是帕斯卡三角。在杨辉三角中，出现次数最多的数字自然是1，这哥们有无穷多个，那么除了1之外，哪个数字出现的最多呢？数一数我们会发现，6出现了3次，不过这不算多，10出现了4次，也还凑合，到底哪一个数最多呢？目前的答案是3003，这个数字在杨辉三角中一共出现了8次。有没有出现次数更多的数字？目前这还是一个谜。

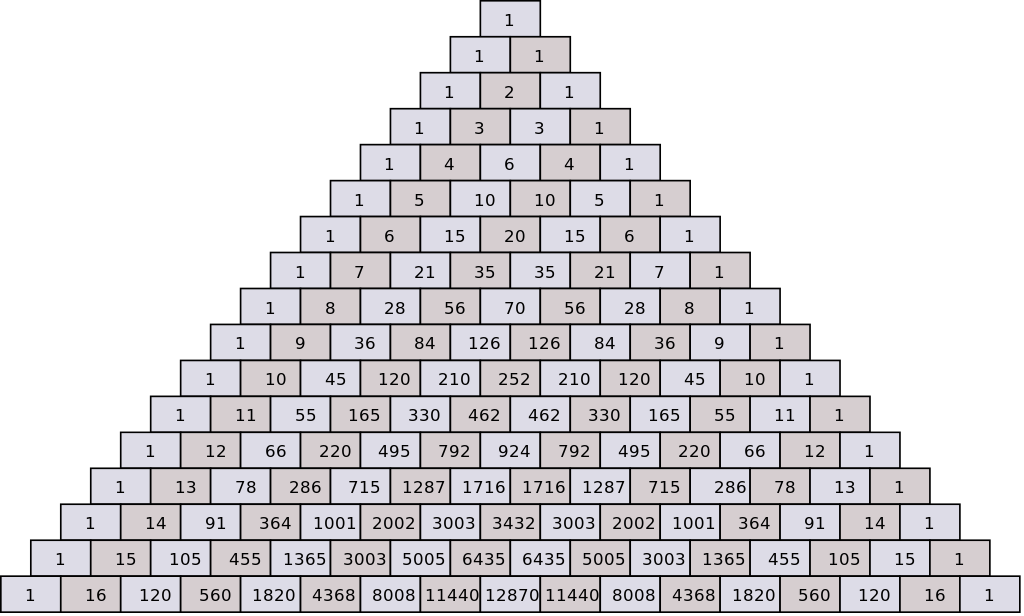
帕斯卡三角

1971年，数学家戴维-辛马斯特通过某种不知道...的方法提出，某个正整数在杨辉三角中出现的次数，存在一个上限，这个上限是多少还不知道，有可能是8，也有可能是10或12。那么到底存不存在这个上限，这个上限又是多少？数学界还没有答案。好了今天就这样吧。