初相

　　在三角函数y=Asin(ωx+φ) （A>0,ω>0 ）中ωx+φ称为相位,当x=0时函数y的相位φ就称为函数y的初相。

　　初相定义

　　在三角函数模型中我们会遇到三角函数图像y=Asin(ωx+φ)。物理中，描述简谐运动的物理量，如振幅、周期、和频率等都是与这个解析式中的常数有关。

　　A就是这个简谐运动的振幅(amplitude of vibration），它是做简谐运动的物体离开平衡位置的最大距离；

　　这个简谐运动的周期（period）是T=2π/ω，这是做间歇运动的物体往复运动一次所需要的时间；

　　这个简谐运动的频率（frequency)由公式f=1/T=|ω|/2π（这里的频率不是指角速率）它是做简谐运动的物体在单位时间内往复运动的次数；

　　ωx+φ称为相位

　　x=0时的相位（ωx+φ=φ）称为初相

　　运算

　　初相的运算

　　（1）三角函数图像向左或向右移动的距离=φ/|ω|（注意移动距离向左符号为正，向右符号为负。谨记左加右减原则）不过这个应用并不广泛。

　　（2）带入运算法：取函数图像上的某点代入函数表达式即可算出初相φ。

　　振动方程与波动方程中的初相

　　振动与波动是医用物理学的重要内容之一 ，也是其中光学的基础 .振动方程与波动方程都可用两种表达式表示：正弦表达式和余弦表达式。同一状态，用两种不同表达式表示 ，其初相值 等均不同。统编教材中振动方程用余弦表达式而波动方程用正弦表达式 ，但对两者的区别 与联系避而不谈 ，极易造成对概念的混乱，同时受课时和专业的限制 ，对两种形式表示的振动 与波动中的初相也不容易彻底讲授清楚 ，针对医药院校医用物理学教学中长期存在的这一问 题可用下述方法解决。

　　振动方程的初相

　　由谐振动微分方程 d²s /dt²+ k²s= 0，得出谐振动的振动方程

　　S = Acos(kt + H) (1) S = Asin(kt + H') (2)

　　(1)、(2)式都是微分方程的解。根据0时刻的相位为初相，所以H与H'均可为初相。初相的意义是决定质点初始位置与状态的。H与H'间的关系可由下式导出：

　　S= Asin(kt+ H' ) = Acos(- kt- H' + c/2)

　　= Acos(kt+ H' - c/2) = Acos(kt+ H)

　　H= H' - c/2

　　正弦可用余弦表示，反过来余弦也可用正弦表示，表示形式不同，初相值不同，总是相差c/2。若用余弦方程中的H定义初相，则正弦方程中的H'不是初相，而是H' - c/2；若用正弦方程中 的H'定义初相，则余弦方程中的H不是初相，而是H+c /2。这种因方程表示形式不同使质点初相值不同的情况很容易导致对初相概念的混乱，进而对振动和波动也不易理解与掌握.H与 H'究竟那一个表达初相更合适，现从下面三个方面进行论证.

　　解析法

　　由表可知，初相为零时，余弦表达的质点处于"正方向端点"，正弦表达的质点处于"平衡位 置，正方向运动"，表明H的起始位置是"正方向端点"，H'的起始位置是"平衡位置，正方向运 动"，显然H与H'差值的根本原因是由于两种表达式的质点起始位置不同而造成的。在一个周 期内，正方向端点只有一个位置，而平衡位置则有两个位置。由此可知，定义H的参考位置只 需一个条件:正方向端点，而定义H'的参考位置需要两个条件:①平衡位置，②向正方向运动. 所以解析法表明：H的参考位置比H'的超前c/2,由H比用H'表达初相更简便;H与H'数值 虽然相差c /2,但其所决定的质点的初相、状态完全相同。

　　矢量法

　　初相H位移S轴正方向与矢量的夹角∠ （见图1）；初相H'：位移S轴正方向沿顺时针方向旋转c/2后与矢量的夹角∠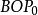 （见图1），或二维直角坐标系（Y轴为位移S轴），X轴的正方向与矢量的夹角为初相∠ （见图2）。因此，矢量法的结论同上述解析法的结论完全一样。

　　曲线法

　　初相H与最靠近坐标原点的波峰相对应的 横轴上的相位值，该点在坐标原点的左边，初相为 超前（H> 0);右边为滞后（H 0);右边为滞后（H'