强影响点

　　强影响点指对多重线性回归模型参数估计有很强影响的数据点。由于多重线性回归采用最小二乘法进行参数估计，此时对所有的记录均一视同仁。当数据库中存在远离多维空间数据主体的记录时，它们将导致拟合的模型偏向该数据点。对于强影响点的识别是进行多重线性回归时应该注意的另一个重要问题。强影响点是对参数估计的稳定性及真实性具有很大影响的数据，对于回归模型数据集中的强影响点是指那些对统计量的取值有非常大的影响力和冲击力的点。由于各个数据点对统计推断的影响大小不相等，为了定量地刻画影响的大小，迄今为止已经提出多种尺度，诸如基于残差的尺度、基于拟合的尺度、基于影响的尺度、基于置信椭圆的尺度、基于似然函数的尺度等。在每一种类型中又可能有不同的统计量，例如基于影响函数就已有多种距离来度量，有Cook距离、Welsch-Kuh距离、Welsch距离修正、Andrews-Pregibon等度量平均拟合距离。由此可见，如何研究影响与从何种角度考虑统计有着密切关系，每一种度量都是某一方面的影响并在具体场合下较为有效。这一方面反映了度量影响问题的复杂性，另一方面也说明了影响分析的研究在统计诊断中是一个较为活跃的方向。此外，还有大量有待研究解决的问题在实际应用中可以选择几种不同的度量对影响进行分析并对各种分析结果加以比较，以期待得到更为全面的结论。其中Cook距离研究比较早，在统计诊断中广泛地为人们所接受1。

　　基本介绍

　　众所周知，线性回归拟合时使用的是最小二乘法，即保证各实测点至直线纵向距离的平方和为最小，这就带来了一个问题：如果存在异常点或离群值，它们离回归直线较远，相应距离的平方就非常的大，为了保证平方和为最小，回归直线不得不强烈的向该点所在方位偏移，显然，这可能会导致错误的分析结论。因此，在回归分析中必须要仔细考虑有无强影响点存在，在样本量比较小的时候尤其应注意该问题。

　　强影响点是指保留该点与删除该点2种情况下建立的回归方程中的回归系数会产生很大差异的点。

　　一般称严重偏离既定模型的数据点为异常点，远离数据主体的点为高杠杆点，对统计推断影响特别大的点为强影响点。其中异常点和高杠杆点都有可能形成强影响点2。

　　强影响点的诊断

　　常用的诊断统计量有：

　　(1)描述性统计量。设投影阵的对角元为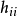 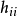， 的值越大，则第i点对回归系数的估计的影响越大（也称该点为杠杆点）；

　　(2)采用Cook距离。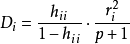 ，式中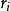 是第i点的标准化残差，该值越大，则第i点对回归系数的估计的影响越大；

　　(3) W-K统计量。 ，式中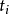 是第i点的外学生化残差，该值越大，则第i点对回归系数的估计的影响越大。

　　若某点为异常点，它可能是强影响点，但也可能不是强影响点，同样，强影响点可能是异常点，也可能不是。

　　当具有异常点或强影响点时，避免它对于估计和拟合的影响的一种方法是删除该点后建立回归方程3。

　　SPSS中对强影响点的诊断有以下几种方法：

　　1.做出散点图，观察有无离群值，它们往往就是强影响点。需要注意的是有些观察值在各个变量单独描述时处在正常范围内，但几个变量联合描述则为异常，例如年龄10岁和体重70公斤单独存在时都不奇怪，但如果同一个人年龄10岁并且体重70公斤显然就不正常了。

　　2.使用Statistic子对话框中的残差诊断指标，如果残差非常大，则相应数据离回归直线较远，可能为强影响点。

　　3.使用Save子对话框中的距离指标和专门的影响力统计量。相应的指标和标准请参见Linear过程的界面说明。

　　4.采用稳健回归方法。对线性回归模型进行诊断时，如果存在多个异常点，使用以上方法容易发生掩盖现象，即未能识别真正的异常点。此时，我们应该考虑采用基于稳健估计的诊断方法。稳健回归方法本身是为了减少异常值对估计值的扰动，属于诊断后的治疗措施。但同时它也可以作为识别异常点的工具。

　　对强影响点的处理对策

　　如果确认存在强影响点，首先应当做的工作是检查原始记录，看看是不是数据录入错误。如果确认数据无误，则分析中可能采取的策略有：

　　去除：如果只有一两个强影响点，可以考虑将其不纳入分析，以确保分析结果能够代表大多数数据的特征。毕竟统计分析是一个少数服从多数的民主过程，可以在分析报告后对这几个强影响点进行单独描述，以全面概括样本信息。

　　变量变换：采用适当的变量变换方法可能会消除强影响点的存在，如倒数变换、对数变换等。这些方法的实质就是弱化极端值的离群趋势，把这些异己分子拉回到集体中来。

　　非参数分析：可以考虑对存在强影响点的变量求秩次，然后采用秩次代替原变量进行回归分析。这是秩分析思想的一种应用，在样本量较大时非常有效。

　　最小一乘法：顾名思义，最小一乘法就是保证各实测点至直线纵向距离绝对值之和为最小，显然比最小二乘法对强影响点有更强的耐受力。该方法在SPSS中采用Nonlinear过程实现。

　　采用加权最小二乘法：利用Weight Estimation过程对强影响点赋予较小的权重，从而削弱对回归方程的影响。这实际上是稳健回归(Robust Regression)思想的一种应用。由于加权最小二乘法中需要找到能够准确预测变异程度的指标，此处可以先进行普通的回归分析，将残差存为新变量，然后将它指定为分析中的加权变量，这样就可能较为准确的预测残差，从而得到较满意的方程2。

　　异常点和强影响点的联系和区别

　　模型中“异常点"和“强影响点"的联系和区别

　　在几乎所有统计诊断中，都将涉及两个基本概念：异常点和强影响点。相关文献对它们作了详细的比较，需要强调的是，宏观经济数据的异常点和强影响点都是一个多维向量，而不是一个单独的数据。这是因为经济系统是一个相互联系、相互制约的整体，在衡量某一个经济变量是否异常时，不能简单地以它自己单独作为判断，同时还必须考虑与其相关的其他经济变量是否能够支撑经济系统的平衡，结合宏观经济统计数据中的异常点和强影响点这两个概念，下面再对二者作一些总结和说明。

　　异常点

　　在回归模型中，异常点是指对既定模型偏离很大的数据点。但究竟偏离到何种程度才算是异常，这就必须对模型误差项的分布有一定的假设(通常假定为正态分布)。另外，尽管异常点的概念看起来很明显，图形上也很直观，但要给它下一个精确的定义却是相当困难的事情。事实上，至今尚无一个公认的统一定义。Bechman和Cook(1983)指出，对于异常点的理解一般有两种情形：第一，子样虽属同一母体，但此值与其他值相比异常地离开，把异常点看成是那些与数据集的总体明显不协调、小概率发生时所产生的数据点。这时，异常点可解释为落在分布的单侧或双侧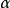 分位点以外的点。第二，把异常点视为杂质点(contaminant)。它与数据集的主体不是来自同一分布，是在绝大多数来自某一共同分布的数据点中掺入的来自另一分布的少量“杂质”。不管采用哪种看法，“异常点”的“异常”之处总是相对于数据集的总体或所假定的模型而言的。在回归模型中，异常点对模型的偏离程度要远比数据主体中的点大4。

　　强影响点

　　数据集合中的强影响点是指那些对统计量的取值有非常大的影响的点。在分析影响大小时，有几个基本问题需要考虑。首先必须明确是对哪一个统计量的影响?一般来讲，对于既定模型，通常总是选择几个有兴趣的统计量，然后考察数据点对它们的影响。其次必须确定度量影响的尺度是什么?为了定量地刻画影响的大小，迄今为止已提出多种尺度。例如，基于残差的尺度、基于拟合的尺度、基于影响函数的尺度、基于置信域的尺度、基于似然函数的尺度等。在每一种类型中又可能有不同的统计量，例如基于影响函彭就已提出多种“距离”来度量，有cook距离、welsch-kuh距离、修正的cook距离等。可见，如何研究影响与从何种角度考虑统计问题有密切关系。每一种度量都是着眼于某一方面的影响，并在某种具体场合下较为有效。这一方面反映了度量影响问题的复杂性，在实际应用中，可以选择几种不同的度量对影响进行分析并对各种分析结果加以比较，以期待得到更为全面的结论。这里需要强调和说明的是，宏观经济统计数据中的强影响点研究的前提条件是建立在正确的计量经济模型基础上的，因此模型的设定除了一般统计模型所必须的条件要求外，同时还必须具有明确的经济意义。

　　如同对待异常点的处理一样，对已判定的强影响点必须慎重处理。强影响点通常是数据集合中更为重要的数据点，它往往能提供比一般数据点更多的信息，因此须引起特别注意。同时，强影响点和异常点是两个不同的概念，它们之间有一定的联系，也有区别。强影响点可能同时又是异常点也可能不是；反之，异常点可能同时又是强影响点也可能不是4。

　　本词条内容贡献者为:

　　刘军 - 副研究员 - 中国科学院工程热物理研究所